题目内容
1.边长为1的等边三角形ABC中,沿BC边高线AD折起,使得折后二面角B-AD-C为60°,点D到平面ABC的距离为$\frac{\sqrt{15}}{10}$.分析 根据条件确定AE为点A到直线BC的距离,DH为点D到面ABC的距离,然后利用边长关系进行求值即可.
解答 解:如图,过D点作DE⊥BC,连AE,则AE⊥BC,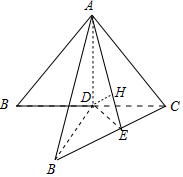
∴AE为点A到直线BC的距离,
在直角三角形ADE中,AE=$\sqrt{A{D}^{2}+D{E}^{2}}$=$\sqrt{(\frac{\sqrt{3}}{2})^{2}+(\frac{\sqrt{3}}{4})^{2}}=\frac{\sqrt{15}}{4}$.
又BC面ADE,且BC?面ABC,
∴面ABC⊥面ADE,AE为高线,作DH⊥AE于H,则DH⊥面ABC,
∴DH为点D到面ABC的距离,
由DH•AE=AD•DE,得DH=$\frac{\frac{\sqrt{3}}{2}×\frac{\sqrt{3}}{4}}{\frac{\sqrt{15}}{4}}$=$\frac{\sqrt{15}}{10}$.
故答案为:$\frac{\sqrt{15}}{10}$.
点评 本题主要考查空间点到直线和点到平面的距离,利用距离公式进行求解,考查学生的运算能力,是中档题.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
11.函数f(x)=x-$\frac{2}{x}$的图象关于( )
| A. | y轴对称 | B. | 原点对称 | C. | 直线y=x对称 | D. | 直线y=-x对称 |
12.已知函数$f(x)=\left\{\begin{array}{l}a{x^2}+1,({x≥0})\\(a+3){e^{ax}},({x<0})\end{array}\right.$为R上的单调函数,则实数a的取值范围是( )
| A. | [-1,0) | B. | (0,+∞) | C. | [-2,0) | D. | (-∞,-2) |