题目内容
4．从3名男同学和2名女同学中任选2名参加体能测试，则恰有1名男同学参加体能测试的概率为$\frac{3}{5}$．（结果用最简分数表示）分析 先求出基本事件总数n=${C}_{5}^{2}$=10，再求出恰有1名男同学参加体能测试包含的基本事件的个数m=${C}_{2}^{1}{C}_{3}^{1}=6$，由此能求出恰有1名男同学参加体能测试的概率．
解答 解：从3名男同学和2名女同学中任选2名参加体能测试，
基本事件总数n=${C}_{5}^{2}$=10，
恰有1名男同学参加体能测试包含的基本事件的个数m=${C}_{2}^{1}{C}_{3}^{1}=6$，
∴恰有1名男同学参加体能测试的概率为p=$\frac{m}{n}=\frac{6}{10}=\frac{3}{5}$．
故答案为：$\frac{3}{5}$．
点评 本题考查概率的求法，是基础题，解题时要认真审题，注意等可能事件概率计算公式的合理运用．
练习册系列答案
相关题目
某市国庆节7天假期的楼房认购量（单位：套）与成交量（单位：套）的折线图如图所示，小明同学根据折线图对这7天的认购量与成交量作出如下判断：①日成交量的中位数是16；②日成交量超过日平均成交量的有2天；③认购量与日期正相关；④10月7日认购量的增幅大于10月7日成交量的增幅．上述判断中错误的个数为（ ）
12．公差为2的等差数列{an}的前n项和为Sn．若S3=12，则a3=（ ）
| A． | 4 | B． | 6 | C． | 8 | D． | 14 |
19．
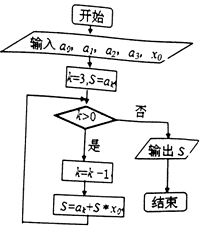秦九韶是我国南宋时代的数学家，其代表作《数书九章》是我国13世纪数学成就的代表之一；如图是秦九韶算法的一个程序框图，则输出的S为（ ）
秦九韶是我国南宋时代的数学家，其代表作《数书九章》是我国13世纪数学成就的代表之一；如图是秦九韶算法的一个程序框图，则输出的S为（ ）| A． | a1+x0（a3+x0（a0+a2x0））的值 | B． | a3+x0（a2+x0（a1+a0x0））的值 | ||
| C． | a0+x0（a1+x0（a2+a3x0））的值 | D． | a2+x0（a0+x0（a3+a1x0））的值 |
9．若函数f（x）=2sinωx（0＜ω＜1）在区间$[{0，\frac{π}{3}}]$上的最大值为1，则ω=（ ）
| A． | $\frac{1}{4}$ | B． | $\frac{1}{3}$ | C． | $\frac{1}{2}$ | D． | $\frac{{\sqrt{3}}}{2}$ |
2．已知命题p：1∈{x|x2-2x+1≤0}，命题q：?x∈[0，1]，x2-1≥0，则下列命题是真命题的是（ ）
| A． | p∧q | B． | ￢p∧（￢q） | C． | p∨q | D． | ￢p∨q |