题目内容

8．已知方程x2+（4+i）x+4+ai=0（a∈R）有实根b，且z=a+bi，则复数z的共轭复数等于（　　）
A．2-2iB．2+2iC．-2+2iD．-2-2i

分析 由复数相等的意义将方程x2+（4+i）x+4+ai=0（a∈R）转化为实系数方程，解方程求出两根．

解答 解：方程x2+（4+i）x+4+ai=0（a∈R）可以变为x2+4x+4+i（x+a）=0，
 由复数相等的意义得$\left\{\begin{array}{l}{{x}^{2}+4x+4=0}\\{x+a=0}\end{array}\right.$解得x=-2，a=2，
 方程x2+（4+i）x+4+ai=0（a∈R）有实根b，故b=-2，
 所以复数z=2-2i，
所以复数z的共轭复数等于2+2i
 故选：B．

点评 本题考查复数相等的意义，两个复数相等，则它们的实部与实部相等，虚部与虚部相等．

练习册系列答案
相关题目
14．若复数z满足$\frac{1-z}{1+z}=i$，则|$\overline{z}$-2|的值为$\sqrt{5}$．
19．已知A，B，C不共线，对空间任意一点O，若$\overrightarrow{OP}$=$\frac{1}{2}$$\overrightarrow{OA}$+（$\frac{1}{4}$-λ）$\overrightarrow{OB}$+（λ+$\frac{1}{4}$）$\overrightarrow{OC}$成立，则“λ=1”是“P，A，B，C四点共面”的（　　）
A．充分不必要条件B．必要不充分条件
C．充要条件D．既非充分也非必要条件
16．已知函数f（x）=|x-2|．
（1）若对任意的a，b，c∈R（a≠c），不等式$\frac{1}{2}$f（m）≤$\frac{|a-b|+|c-d|}{|a-c|}$恒成立，求实数m的最大值；
（2）在（1）的条件下，解不等式f（x）≤2-|x-m|．
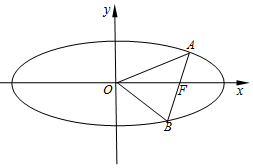3．如图，在平面直角坐标系xOy中，已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的焦距为2，过右焦点F的直线l交椭圆于A、B两点，当l与x轴垂直时，AB长为$\frac{{4\sqrt{3}}}{3}$．   
（1）求椭圆的标准方程；
（2）若椭圆上存在一点P，使得$\overrightarrow{OP}=\overrightarrow{OA}+\overrightarrow{OB}$，求直线l的斜率．
13．已知集合M={x|x2＜1}，N={x|2x＞1}，则M∩N=（　　）
A．∅B．{x|0＜x＜1}C．{x|x＜0}D．{x|x＜1}
20．已知集合A={x|x2-3x+2＜0}，B={x|a-1＜x＜3a+1}．
（1）当a=$\frac{1}{4}$时，求A∩B；
（2）命题p：x∈A，命题q：x∈B，若q是p的必要条件，求实数a的取值范围．
17．已知集合A={0，2，4，6}，B={x∈N|2x≤33}，则集合A∩B的子集个数为（　　）
A．6B．7C．8D．4
18．设F为抛物线y2=4x的焦点，A，B，C为该抛物线上不同的三点，$\overrightarrow{FA}+\overrightarrow{FB}+\overrightarrow{FC}=\overrightarrow 0$，O为坐标原点，且△OFA、△OFB、△OFC的面积分别为S1、S2、S3，则$S_1^2+S_2^2+S_3^2$=3．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网