题目内容
已知数列{an}的前n项和Sn=10n-n2,(n∈N*).
(1)求a1和an;
(2)记bn=|an|,求数列{bn}的前n项和.
解析 (1)∵Sn=10n-n2,∴a1=S1=10-1=9.
∵Sn=10n-n2,当n≥2,n∈N*时,
Sn-1=10(n-1)-(n-1)2=10n-n2+2n-11,
∴an=Sn-Sn-1=(10n-n2)-(10n-n2+2n-11)
=-2n+11.
又n=1时,a1=9=-2×1+11,符合上式.
则数列{an}的通项公式为an=-2n+11(n∈N*).
(2)∵an=-2n+11,∴bn=|an|=
设数列{bn}的前n项和为Tn,
n≤5时,Tn= =10n-n2;
=10n-n2;
n>5时Tn=T5+ =25+
=25+ =25+(n-5)2=n2-10n+50,
=25+(n-5)2=n2-10n+50,
∴数列{bn}的前n项和Tn=

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案
相关题目
 ,其中λ,m,α为实数.若a=2b,则
,其中λ,m,α为实数.若a=2b,则 的取值范围是( ).
的取值范围是( ).
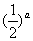 =
=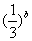 ,则a>b>0;
,则a>b>0;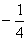 ;
; 表示的平面区域的面积为4,点
表示的平面区域的面积为4,点 在所给平面区域内,则
在所给平面区域内,则 的最大值为 .
的最大值为 .