题目内容
已知函数f（x）=9-x-2×31-x-27，x∈[-2，2]，求函数f（x）的值域．
考点：函数的值域
专题：函数的性质及应用
分析：令t=3-x，集合x的范围，求出t的范围，将函数f（x）转化为f（t）=t2-6t-27=（t-3）2+18，根据二次函数的性质，从而求出函数的值域．
解答：
解：f（x）=9-x-2×31-x-27=3-2x-6•3-x-27，
令t=3-x，x∈[-2，2]，∴t∈[
，9]，
∴f（t）=t2-6t-27=（t-3）2+18，
∴f（t）min=f（3）=18，f（t）max=f（9）=54，
∴f（x）的值域是：[18，54]．
令t=3-x，x∈[-2，2]，∴t∈[
| 1 |
| 9 |
∴f（t）=t2-6t-27=（t-3）2+18，
∴f（t）min=f（3）=18，f（t）max=f（9）=54，
∴f（x）的值域是：[18，54]．
点评：本题考查了复合函数的值域问题，考查了二次函数的性质，是一道基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
某扇形的圆心角为30°，半径为2，那么该扇形弧长为（ ）
A、
| ||
B、
| ||
C、
| ||
| D、60 |
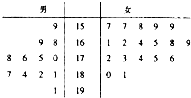某县职工运动会将在本县一中运动场隆重召开，为了搞好接待工作，执委会在一中招募了12名男性志愿者和18名女性志愿者，调查发现，这30名志愿者的身高如图：（单位：cm）