题目内容
19. 如图,菱形ABCD的边长为2,△BCD为正三角形,现将△BCD沿BD向上折起,折起后的点C记为C′,且CC′=$\sqrt{3}$,连接CC′,E为CC′的中点.
如图,菱形ABCD的边长为2,△BCD为正三角形,现将△BCD沿BD向上折起,折起后的点C记为C′,且CC′=$\sqrt{3}$,连接CC′,E为CC′的中点.文科:(1)求证:AC′∥平面BDE;
(2)求证:CC′⊥平面BDE;
(3)求三棱锥C′-BCD的体积.
分析 (1)连接OE,则OE∥AC′,由此能证明AC′∥平面BDE.
(2)由翻折前后可知BE⊥CC′,DE⊥CC′,由此能证明CC′⊥平面BDE.
(3)连接OE,三棱锥C′-BCD的体积:${V}_{{C}^{'}-BCD}={V}_{{C}^{'}-BDE}+{V}_{C-BDE}$,由此能求出结果.
解答 证明:(1)连接OE,则在菱形ABCD中,O为AC中点,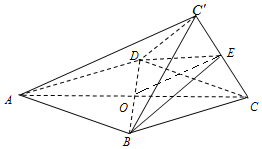
又E为CC′的中点,∴OE∥AC′,
∵OE?平面BDE,AC′?平面BDE,
∴AC′∥平面BDE.
(2)由翻折前后可知:
BC=BC′,DC=DC′,
又E为CC′中点,∴BE⊥CC′,DE⊥CC′,
又BE∩DE=E,∴CC′⊥平面BDE.
解:(3)连接OE,则由(2)知△CEO为直角三角形,OE⊥BD,
∴BD=2,OE=$\frac{3}{2}$,
∴三棱锥C′-BCD的体积:
${V}_{{C}^{'}-BCD}={V}_{{C}^{'}-BDE}+{V}_{C-BDE}$
=$\frac{1}{3}×{S}_{△BDE}×E{C}^{'}+\frac{1}{3}×{S}_{△BDE}×EC$
=$\frac{1}{3}{S}_{△BDE}×C{C}^{'}$
=$\frac{1}{3}×\frac{1}{2}×BD×OE×C{C}^{'}$
=$\frac{\sqrt{3}}{2}$.
点评 本题考查线面平行的证明,考查线面垂直的证明,考查三棱锥的体积的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
9.设集合A={x|x3-2x2-x+2=0},下列哪个元素不属于集合A( )
| A. | 1 | B. | -1 | C. | 2 | D. | -2 |
10.等差数列{an},{bn}的前n项之和分别为Sn,Tn,若$\frac{{a}_{n}}{{b}_{n}}$=$\frac{2n}{3n+1}$,则$\frac{{S}_{21}}{{T}_{21}}$的值为( )
| A. | $\frac{13}{15}$ | B. | $\frac{23}{35}$ | C. | $\frac{11}{17}$ | D. | $\frac{4}{9}$ |