题目内容
设某大学的女生体重 (单位:kg)与身高
(单位:kg)与身高 (单位:cm)具有线性相关关系,根据一组样本数据(
(单位:cm)具有线性相关关系,根据一组样本数据( )(
)( =1,2,…,n),用最小二乘法建立的回归方程为
=1,2,…,n),用最小二乘法建立的回归方程为 =0.85
=0.85 —85.71,则下列结论其中正确的个数是( )
—85.71,则下列结论其中正确的个数是( )
① y与x具有负的线性相关关系
② 回归直线过样本点的中心( ,
, )
)
③ 若该大学某女生身高增加1cm,则其体重约增加0.85kg
④ 若该大学某女生身高为170cm,则可断定其体重必为58.79kg
| A.0 | B.1 | C. 2 | D. 3 |
C
解析试题分析:x的系数为正,所以y与x具有正的线性相关关系,①错误;②正确,回归直线必过中心点
③正确④错误,通过回归方程计算出来的结果是估计值,不是精确值
考点:回归直线方程
点评:在回归直线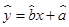 中
中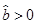 则y与x正相关,
则y与x正相关,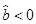 则y与x负相关,回归直线过中心点
则y与x负相关,回归直线过中心点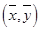

练习册系列答案
相关题目
在回归直线方程 ( )
( )
A.当 , , 的平均值 的平均值 |
B.当 变动一个单位时, 变动一个单位时, 的实际变动量 的实际变动量 |
C.当 变动一个单位时, 变动一个单位时, 的平均变动量 的平均变动量 |
D.当 变动一个单位时, 变动一个单位时, 的平均变动量 的平均变动量 |
在一次对“学生的数学成绩与物理成绩是否有关”的独立性检验的试验中,由 列联表算得
列联表算得 的观测值
的观测值 ,参照附表:
,参照附表:
 | 0.050 | 0.010 | 0.001 |
 | 3.841 | 6.635 | 10.828 |
判断在此次试验中,下列结论正确的是( )
A. 有99.9%以上的把握认为“数学成绩与物理成绩有关”
B. “数学成绩与物理成绩有关” 的概率为99%
C. 在犯错误的概率不超过0.01的前提下,认为“数学成绩与物理成绩有关”
D. 在犯错误的概率不超过0.001的前提下,认为“数学成绩与物理成绩有关”
设有一个回归方程为 ,变量
,变量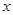 增加一个单位时,则
增加一个单位时,则
A.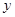 平均增加 平均增加 个单位 个单位 | B.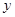 平均增加2个单位 平均增加2个单位 |
C.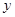 平均减少 平均减少 个单位 个单位 | D.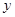 平均减少2个单位 平均减少2个单位 |
四个变量 ,
, ,
,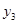 ,
,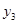 随变量
随变量 变化的数据如下表:
变化的数据如下表:
 | 0 | 5 | 10 | 15 | 20 | 25 |
 | 5 | 130 | 505 | 1130 | 2005 | 3130 |
 | 5 | 94.478 | 1785.2 | 33733 | 6.37 | 1.2 |
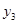 | 5 | 30 | 55 | 80 | 105 | 130 |
 | 5 | 2.3107 | 1.4295 | 1.11407 | 1.0461 | 1.0151 |
 呈指数型函数变化的变量是( )
呈指数型函数变化的变量是( )A.
 B.
B. C.
C.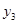 D.
D.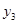
设有一个回归方程为y=2-3x,变量x增加1个单位时,则y平均( )
| A.增加2个单位 | B.减少2个单位 | C.增加3个单位 | D.减少3个单位 |
对于一组数据 (
( ),如果将它们改变为
),如果将它们改变为 (
( ),其中
),其中 ,下列结论正确的是( )
,下列结论正确的是( )
| A.平均数与方差均不变 | B.平均数变了,而方差保持不变 |
| C.平均数不变,而方差变了 | D.平均数与方差均发生了变化 |
在如下图所示的各图中,两个变量具有相关关系的是( )
| A.(1)(2) | B.(1)(3) |
| C.(2)(4) | D.(2)(3) |
对变量 有观测数据
有观测数据 …,10),得散点图(1)所示.对变量
…,10),得散点图(1)所示.对变量 有观测数据
有观测数据 ,…,10),得散点图(2).由这两个散点图可以判断
,…,10),得散点图(2).由这两个散点图可以判断
A.变量 与 与 正相关, 正相关,  与 与 正相关 正相关 | B.变量 与 与 正相关, 正相关,  与 与 负相关 负相关 |
C.变量 与 与 负相关, 负相关,  与 与 正相关 正相关 | D.变量 与 与 负相关, 负相关,  与 与 负相关 负相关 |