题目内容
在回归直线方程
（ ）
A．当 ， 的平均值 |
B．当 变动一个单位时，的实际变动量 |
| C．当变动一个单位时，的平均变动量 |
| D．当变动一个单位时，的平均变动量 |
D
解析试题分析：根据所给的回归直线方程，把自变量由x变化为x+1，表示出变化后的y的值，两个式子相减，得到y的变化. 解：∵直线回归方程为 
=a+bx①,∴2=a+b（x+1）②,∴②-①得：2-1=b，即y平均减少b个单位，∴在回归直线方程=a+bx中，回归系数b表示：当x变动一个单位时，y的平均变动量．故选D．
考点：线性回归方程
点评：本题考查线性回归方程的意义，要注意加上平均变化的字样，本题是一个基础题．
练习册系列答案
相关题目
次综合测评中的成绩，其中一个数字被污损.则甲的平均成绩超过 乙的平均成绩的概率为
为了解某种轮胎的性能，随机抽取了8个进行测试，其最远里程数（单位：1000km）为：96, 112, 97, 108, 99, 104, 86, 98，则他们的中位数是( )
| A．100 | B．99 | C．98.5 | D．98 |
下图是甲、乙两名篮球运动员在以往几场篮球赛中得分的茎叶图，设
甲、乙两组数据的平均数分别为
，
，中位数分别为m甲，m乙，则
| A．<，m甲> m乙 | B．<，m甲< m乙 |
| C．，m甲> m乙 | D．>，m甲< m乙 |
工人月工资y（元）与劳动生产率x（千元）变化的回归方程
，下列判断正确的是 ( )
①劳动生产率为1千元时，工资约为130元
②劳动生产率提高1千元时，月工资约提高80元
③劳动生产率提高1千元时，月工资约提高130元
④当月工资为210元时，劳动生产率约为2千元
| A．① ② | B．① ② ④ | C．② ④ | D．① ② ③ ④ |
某商品销售量y(件)与销售价格x(元/件)负相关，则其回归方程可能是( )
A． ＝－10x＋200 | B．＝10x＋200 |
| C．＝－10x－200 | D．＝10x－200 |
根据一组样本数据
的散点图分析存在线性相关关系，求得其回归方程
，则在样本点
处的残差为（ ）
A． | B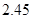． | C． | D． |
（单位：kg）与身高
（单位：cm）具有线性相关关系，根据一组样本数据(
)（
=1，2，…，n），用最小二乘法建立的回归方程为
=0.85
，
）