题目内容
6．为了对新研发的一种产品进行合理定价，将该产品按事先拟定的价格进行试销，得到如表数据：| 单价x（元） | 8 | 8.2 | 8.4 | 8.6 | 8.8 | 9 |
| 销量y（件） | 90 | 84 | 83 | m | 75 | 68 |
（1）试求表格中m的值；
（2）预计在今后的销售中，销量与单价仍然服从建立的回归方程，且该产品的成本是5元/件，为使工厂获得最大利润，该产品的单价应定为多少元？（利润=销售收入-成本）
分析 （1）利用平均数公式求得样本中心点的坐标，根据样本中心点在回归直线上，求m的值；
（2）根据题意构造函数，利用函数求得函数值取得最大值时的定价．
解答 解：（1）∵$\overline{x}$=8.5，回归直线方程为$\widehaty=-20x+250$，
∴$\overline{y}$=80，
∴$\frac{1}{6}$（90+84+83+m+75+68）=80，∴m=80；--（6分），
（2）设工厂获得的利润为L元，则依题意得：L=（x-5）（-20x+250）--（8分），
=-20（x2-17.5x+62.5）=-20（x-8.75）2+281.25，（5＜x＜12.5），--（10分），
∴当x=8.75时，L取得最大值．--（11分），
故当单价定为8.75元/件时，工厂可获得最大利润．--（12分）
点评 本题考查了回归直线的性质及回归系数的求法，考查了回归分析的应用，熟练掌握回归分析的思想方法是解题的关键．
练习册系列答案
相关题目
17．设F1，F2分别为$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）双曲线a≥1的左、右焦点，双曲线上存在一点P使得（|PF1|-|PF2|）2=b2-3ab，则该双曲线的离心率为（ ）
| A． | $\sqrt{2}$ | B． | $\sqrt{15}$ | C． | 4 | D． | $\sqrt{17}$ |
14．定义A*B，B*A，C*D，D*A的运算分别对应图2中的（1）（2）（3）（4），那么，图1中（A）（B）可能是下列的运算的结果（ ）
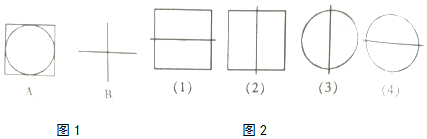
| A． | B*D，A*D | B． | B*D，A*C | C． | B*C，A*D | D． | C*D，A*D |
18．直线l过点（1，0）且与曲线y=-$\frac{1}{{e}^{x}}$相切，设其倾斜角为α，则α=（ ）
| A． | 30° | B． | 60° | C． | 45° | D． | 135° |