题目内容
设P是双曲线
-
=1(a>0,b>0)上除顶点外的任意一点,F1、F2分别是双曲线的左、右焦点,△PF1F2的内切圆与边F1F2相切于点M,则
•
=( )
| x2 |
| a2 |
| y2 |
| b2 |
| F1M |
| MF2 |
| A.a2 | B.b2 | C.a2+b2 | D.
|
不妨设P是双曲线
-
=1(a>0,b>0)右支上一点,则|PF1|-|PF2|=2a,
∵△PF1F2的内切圆与边F1F2相切于点M,
∴|F1M|-|F2M|=2a,
∵|F1M|+|F2M|=2c,
∴|F1M|=a+c,|F2M|=c-a,
∴
•
=|F1M||F2M|=c2-a2=b2,
故选:B.
| x2 |
| a2 |
| y2 |
| b2 |
∵△PF1F2的内切圆与边F1F2相切于点M,
∴|F1M|-|F2M|=2a,
∵|F1M|+|F2M|=2c,
∴|F1M|=a+c,|F2M|=c-a,
∴
| F1M |
| MF2 |
故选:B.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
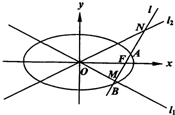

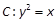 .命题p: 直线l1:
.命题p: 直线l1: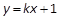 与抛物线C有公共点.命题q: 直线l2:
与抛物线C有公共点.命题q: 直线l2: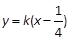 被抛物线C所截得的线段长大于2.若
被抛物线C所截得的线段长大于2.若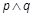 为假,
为假, 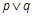 为真,求k的取值范围.
为真,求k的取值范围.