题目内容
8.在棱长为1的正方体ABCD-A1B1C1D1中,点B到A1C1的距离是$\frac{\sqrt{6}}{2}$.分析 以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,利用向量法能求出点B到A1C1的距离.
解答 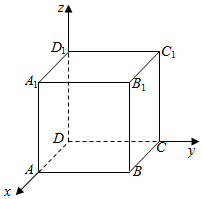 解:以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,
解:以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,
B(1,1,0),A1(1,0,1),C1(0,1,1),
$\overrightarrow{{A}_{1}B}$=(0,1,-1),$\overrightarrow{{A}_{1}{C}_{1}}$=(-1,1,0),
∴点B到A1C1的距离:
d=|$\overrightarrow{{A}_{1}B}$|•$\sqrt{1-[cos<\overrightarrow{{A}_{1}B},\overrightarrow{{A}_{1}{C}_{1}}>]^{2}}$=$\sqrt{2}$•$\sqrt{1-(\frac{1}{\sqrt{2}•\sqrt{2}})^{2}}$=$\frac{\sqrt{6}}{2}$.
故答案为:$\frac{\sqrt{6}}{2}$.
点评 本题考查点到直线的距离的求法,是基础题,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
相关题目
20.若3a2-5b<0,则方程x5+2ax3+2bx+4c=0( )
| A. | 无实根 | B. | 有唯一实根 | C. | 有三个不同实根 | D. | 有五个不同实根 |