题目内容
下列命题中,真命题是( )
| A、?x∈(3,+∞),x2>2x+1 | ||
B、?x0∈[0,
| ||
| C、?x0∈R,x02+x0=-1 | ||
D、?x∈(
|
考点:命题的真假判断与应用
专题:阅读型,简易逻辑
分析:由二次函数的单调性,即可判断A;运用两角和的正弦公式,结合正弦函数的值域,即可判断B;
由二次方程的判别式,即可判断C;运用第二象限的正切和正弦的符号,即可判断D.
由二次方程的判别式,即可判断C;运用第二象限的正切和正弦的符号,即可判断D.
解答:
解:对于A.由于y=x2-2x-1=(x-1)2-2,对称轴为x=1,在(3,+∞)递增,
即有y>(3-1)2-2=2恒成立,则A正确;
对于B.由于y=sinx+cosx=
(
sinx+
cosx)=
sin(x+
)的最大值为
,则B错误;
对于C.由于x2+x+1=0的判别式为1-4=-3<0,则方程无实数解,则C错误;
对于D.当x∈(
,π)时,tanx<0,sinx>0,即tanx<sinx.则D错误.
故选A.
即有y>(3-1)2-2=2恒成立,则A正确;
对于B.由于y=sinx+cosx=
| 2 |
| ||
| 2 |
| ||
| 2 |
| 2 |
| π |
| 4 |
| 2 |
对于C.由于x2+x+1=0的判别式为1-4=-3<0,则方程无实数解,则C错误;
对于D.当x∈(
| π |
| 2 |
故选A.
点评:本题考查全称性命题和存在性命题的真假,注意运用二次函数的单调性和二次方程的判别式,以及三角函数的图象和性质,属于基础题和易错题.

练习册系列答案
相关题目
三棱锥P-ABC的三条侧棱PA、PB、PC两两互相垂直,且长度分别为3、4、5,则三棱锥P-ABC外接球的体积是( )
A、20
| ||||
B、
| ||||
C、
| ||||
| D、50π |
如果命题“p∧q”是假命题,“非q”也是假命题,则( )
| A、命题“非p∨q”是假命题 |
| B、命题“p∨q”是假命题 |
| C、命题“非p∧q”是真命题 |
| D、命题“p∧非q”是真命题 |
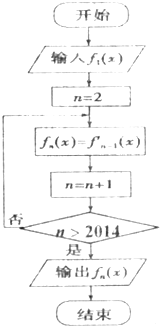 在如图所示的程序框图中,当n∈N*(n>1)时,函数fn(x)等于函数fn-1(x)的导函数,若输入函数f1(x)=sinx+cosx,则输出的函数fn(x)可化为( )
在如图所示的程序框图中,当n∈N*(n>1)时,函数fn(x)等于函数fn-1(x)的导函数,若输入函数f1(x)=sinx+cosx,则输出的函数fn(x)可化为( )A、
| ||||
B、
| ||||
C、-
| ||||
D、-
|
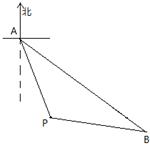 如图,某船在A处看见灯塔P在南偏东15°方向,后来船沿南偏东45°的方向航行30km后,到达B处,看见灯塔P在船的西偏北15°方向,则这时船与灯塔的距离是( )
如图,某船在A处看见灯塔P在南偏东15°方向,后来船沿南偏东45°的方向航行30km后,到达B处,看见灯塔P在船的西偏北15°方向,则这时船与灯塔的距离是( )| A、10km | ||
| B、20km | ||
C、10
| ||
D、5
|
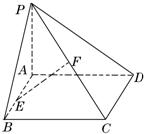 如图,已知矩形ABCD所在平面外一点P,PA⊥平面ABCD,E、F分别是AB、PC的中点.
如图,已知矩形ABCD所在平面外一点P,PA⊥平面ABCD,E、F分别是AB、PC的中点.