题目内容
已知F1,F2是双曲线
-
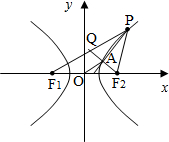
=1(a>0,b>0)的左、右焦点,点P在双曲线上且不与顶点重合,过F2作∠F1PF2的角平分线的垂线,垂足为A.若|OA|=b,则该双曲线的离心率为 .
| x2 |
| a2 |
| y2 |
| b2 |
考点:双曲线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:由题设条件推导出PQ=PF2,由双曲线性质推导出PF1-PQ=QF1=2a,由中位线定理推导出QF1=2a=2OA=2,由此及彼能求出双曲线的离心率.
解答:
 解:∵F1,F2是双曲线
解:∵F1,F2是双曲线
-
=1的左右焦点,
延长F2A交PF1于Q,
∵PA是∠F1PF2的角平分线,∴PQ=PF2,
∵P在双曲线上,∴PF1-PF2=2a,
∴PF1-PQ=QF1=2a,
∵O是F1F2中点,A是F2Q中点,
∴OA是△F2F1Q的中位线,
∴QF1=2a=2OA=2b,
∴a=b,c=
a,
∴双曲线的离心率e=
.
故答案为:
.
 解:∵F1,F2是双曲线
解:∵F1,F2是双曲线| x2 |
| a2 |
| y2 |
| b2 |
延长F2A交PF1于Q,
∵PA是∠F1PF2的角平分线,∴PQ=PF2,
∵P在双曲线上,∴PF1-PF2=2a,
∴PF1-PQ=QF1=2a,
∵O是F1F2中点,A是F2Q中点,
∴OA是△F2F1Q的中位线,
∴QF1=2a=2OA=2b,
∴a=b,c=
| 2 |
∴双曲线的离心率e=
| 2 |
故答案为:
| 2 |
点评:本题考查双曲线的离心率的求法,是中档题,解题时要认真审题,要熟练掌握双曲线的性质.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知{an}是以1为首项的等比数列,若a7•a11=100,则a9的值是( )
| A、-10 | B、10 |
| C、±10 | D、不确定 |
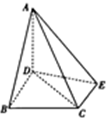 在三棱椎A-BCD中,AB=BC=4,AD=BD=CD=2
在三棱椎A-BCD中,AB=BC=4,AD=BD=CD=2