题目内容
在平面直角坐标系中,动点P(x,y)到两条坐标轴的距离之和等于它到点(1,1)的距离,记点P的轨迹为曲线W,给出下列四个结论:
①曲线W关于原点对称;
②曲线W关于直线y=x对称;
③曲线W与x轴非负半轴,y轴非负半轴围成的封闭图形的面积小于
;
④曲线W上的点到原点距离的最小值为2-
其中,所有正确结论的序号是 .
①曲线W关于原点对称;
②曲线W关于直线y=x对称;
③曲线W与x轴非负半轴,y轴非负半轴围成的封闭图形的面积小于
| 1 |
| 2 |
④曲线W上的点到原点距离的最小值为2-
| 2 |
其中,所有正确结论的序号是
考点:轨迹方程
专题:计算题,圆锥曲线的定义、性质与方程
分析:根据动点P(x,y)到两条坐标轴的距离之和等于它到点(1,1)的距离,可得曲线方程,作出曲线的图象,即可得到结论.
解答:
 解:∵动点P(x,y)到两条坐标轴的距离之和等于它到点(1,1)的距离,
解:∵动点P(x,y)到两条坐标轴的距离之和等于它到点(1,1)的距离,
∴|x|+|y|=
,
∴|xy|+x+y-1=0,
∴xy>0,(x+1)(y+1)=2或xy<0,(y-1)(1-x)=0,
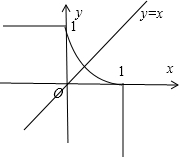
函数的图象如图所示
∴曲线W关于直线y=x对称;
曲线W与x轴非负半轴,y轴非负半轴围成的封闭图形的面积小于
;
由y=x与(x+1)(y+1)=2联立可得x=
-1,∴曲线W上的点到原点距离的最小值为
(
-1)=2-
,
∴所有正确结论的序号是②③④.
故答案为:②③④.
 解:∵动点P(x,y)到两条坐标轴的距离之和等于它到点(1,1)的距离,
解:∵动点P(x,y)到两条坐标轴的距离之和等于它到点(1,1)的距离,∴|x|+|y|=
| (x-1)2+(y-1)2 |
∴|xy|+x+y-1=0,
∴xy>0,(x+1)(y+1)=2或xy<0,(y-1)(1-x)=0,
函数的图象如图所示
∴曲线W关于直线y=x对称;
曲线W与x轴非负半轴,y轴非负半轴围成的封闭图形的面积小于
| 1 |
| 2 |
由y=x与(x+1)(y+1)=2联立可得x=
| 2 |
| 2 |
| 2 |
| 2 |
∴所有正确结论的序号是②③④.
故答案为:②③④.
点评:本题考查轨迹方程,考查数形结合的数学思想,求出轨迹方程,正确作出曲线的图象是关键.

练习册系列答案
相关题目
若复数z=
,则|
|等于( )
| 2i |
| 1-i |
. |
| z |
A、
| ||||
B、
| ||||
| C、1 | ||||
D、
|
双曲线焦点在y轴上,且a+c=9,b=3,则它的标准方程是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
若集合A={x|x(x-2)>0},B={x||x+1|<2},则A∩B=( )
| A、(-3,2) |
| B、(-3,0) |
| C、(0,2) |
| D、(1,2) |