题目内容
7.已知数列{an}中,a1=3,且 an-1-an=$\frac{1}{3}$nan-1an(n≥2,n∈N*).(1)证明:an≠0(a≠2,n∈N*);
(2)设b=$\frac{1}{{a}_{n}}$,求数列{bn}的通项公式;
(3)记数列{an}的前n项和为Tn,求证:Tn<6(n∈N*)
分析 (1)运用恒等式$\frac{1}{{a}_{n}}$=($\frac{1}{{a}_{n}}$-$\frac{1}{{a}_{n-1}}$)+($\frac{1}{{a}_{n-1}}$-$\frac{1}{{a}_{n-2}}$)+…+($\frac{1}{{a}_{3}}$-$\frac{1}{{a}_{2}}$)+($\frac{1}{{a}_{2}}$-$\frac{1}{{a}_{1}}$)+$\frac{1}{{a}_{1}}$,由此利用累加法和等差数列通项公式求出$\frac{1}{{a}_{n}}$=$\frac{n(n+1)}{6}$,从而能求出an=$\frac{6}{n(n+1)}$,即有an≠0;
(2)由(1)可得bn;
(3)由an=$\frac{6}{n(n+1)}$=6($\frac{1}{n}$-$\frac{1}{n+1}$),再由数列的求和方法:裂项相消求和和不等式的性质,即可得证.
解答 解:(1)证明:∵a1=3,an-1-an=$\frac{1}{3}$nan-1an,
∴$\frac{1}{{a}_{n}}$-$\frac{1}{{a}_{n-1}}$=$\frac{1}{3}$n,n≥2,
∴$\frac{1}{{a}_{n}}$=($\frac{1}{{a}_{n}}$-$\frac{1}{{a}_{n-1}}$)+($\frac{1}{{a}_{n-1}}$-$\frac{1}{{a}_{n-2}}$)+…+($\frac{1}{{a}_{3}}$-$\frac{1}{{a}_{2}}$)+($\frac{1}{{a}_{2}}$-$\frac{1}{{a}_{1}}$)+$\frac{1}{{a}_{1}}$
=$\frac{1}{3}$[n+(n-1)+(n-2)+…+3+2+1]
=$\frac{1}{3}$×$\frac{1}{2}$n(n+1)=$\frac{n(n+1)}{6}$,
∴an=$\frac{6}{n(n+1)}$(n≥2),
对n=1也成立,即有an≠0;
(2)由(1)可得bn=$\frac{1}{{a}_{n}}$=$\frac{n(n+1)}{6}$;
(3)证明:前n项和为Tn=a1+a2+…+an=$\frac{6}{1•2}$+$\frac{6}{2•3}$+…+$\frac{6}{n(n+1)}$
=6(1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+…+$\frac{1}{n}$-$\frac{1}{n+1}$)=6(1-$\frac{1}{n+1}$)<6,
则Tn<6(n∈N*).
点评 本题考查数列的通项公式的求法,数列的求和方法:裂项相消求和和不等式的证明,是中档题,解题时要认真审题,注意累加法的合理运用.

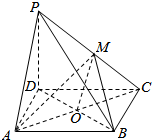 如图,已知P为平行四边形ABCD所在平面外一点,M是线段PC的中点.
如图,已知P为平行四边形ABCD所在平面外一点,M是线段PC的中点.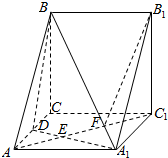 三棱柱ABC-A1B1C1中,D是AC的中点,A1D与AC1交于点E,F在线段AC1上,且AF=2FC1.
三棱柱ABC-A1B1C1中,D是AC的中点,A1D与AC1交于点E,F在线段AC1上,且AF=2FC1.