题目内容
1．正方体A1B1C1D1-ABCD中，BD与B1C所成的角是（ ）| A． | 90° | B． | 60° | C． | 45° | D． | 30° |
分析 连接B1D1和D1C，由BD∥B1D1，知∠D1B1C就是异面直线DB与B1C所成角．由△D1B1C是等边三角形，知异面直线DB与B1C所成角为60°．
解答 解：如图，连接B1D1，则DB∥D1B1，
则∠D1B1C为异面直线BD与B1C所成的角，
连接D1C，在△D1B1C中，D1B1=B1C=CD1，
则∠D1B1C=60°，
因此异面直线BD与B1C所成的角为60°．
故选：B．
点评 本题考查的知识点是空间中直线与直线之间的位置关系，异面直线及其所成的角，难度中档．
练习册系列答案
备战中考寒假系列答案
相关题目
11．设f（x）=|sinπx|，则f（1）+f（2）+f（3）+…+f（2010）=（ ）
| A． | 0 | B． | $\sqrt{3}$ | C． | -$\sqrt{3}$ | D． | 1 |
6．已知-$\frac{π}{6}$＜α＜$\frac{π}{6}$，且cos（α+$\frac{π}{6}$）=$\frac{4}{5}$，则sin（2α+$\frac{π}{12}$）的值为（ ）
| A． | $\frac{17\sqrt{2}}{50}$ | B． | $\frac{31\sqrt{2}}{50}$ | C． | $\frac{7\sqrt{2}}{10}$ | D． | $\frac{\sqrt{2}}{10}$ |
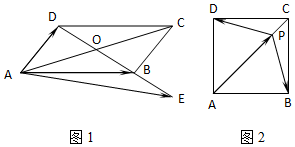（1）如图1，在平行四边形ABCD中，点E是对角线DB的延长线上一点，且OB=BE．记$\overrightarrow{AB}=\overrightarrow a\;，\;\overrightarrow{AD}=\overrightarrow b$，试用向量$\overrightarrow a\;，\;\overrightarrow b$表示$\overrightarrow{AE}$．