题目内容
5.已知sin(α-$\frac{π}{3}$)=$\frac{1}{3}$,则cos(α+$\frac{π}{6}$)=( )| A. | $\frac{2\sqrt{2}}{3}$ | B. | $\frac{1}{3}$ | C. | -$\frac{2\sqrt{2}}{3}$ | D. | -$\frac{1}{3}$ |
分析 利用两角和与差的三角函数化简已知条件,然后求解所求表达式的值.
解答 解:sin(α-$\frac{π}{3}$)=$\frac{1}{3}$,即$\frac{1}{2}sinα-\frac{\sqrt{3}}{2}cosα=\frac{1}{3}$.
cos(α+$\frac{π}{6}$)=$\frac{\sqrt{3}}{2}cosα-\frac{1}{2}sinα$=$-(\frac{1}{2}sinα-\frac{\sqrt{3}}{2}cosα)$=$-\frac{1}{3}$.
故选:D.
点评 本题考查两角和与差的三角函数,诱导公式的应用,基本知识的考查,是基础题.

练习册系列答案
相关题目
16. 某几何体的三视图如图所示,则该几何体中,最大侧面的面积为( )
某几何体的三视图如图所示,则该几何体中,最大侧面的面积为( )
 某几何体的三视图如图所示,则该几何体中,最大侧面的面积为( )
某几何体的三视图如图所示,则该几何体中,最大侧面的面积为( )| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{5}}{2}$ | D. | $\frac{\sqrt{6}}{2}$ |
10.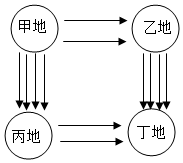 如图,从甲地到乙地有2条路,从乙地到丁地有3条路;从甲地到丙地有4 条路,从丙地到丁地有2条路,则从甲地到丁地不同的路有( )
如图,从甲地到乙地有2条路,从乙地到丁地有3条路;从甲地到丙地有4 条路,从丙地到丁地有2条路,则从甲地到丁地不同的路有( )
 如图,从甲地到乙地有2条路,从乙地到丁地有3条路;从甲地到丙地有4 条路,从丙地到丁地有2条路,则从甲地到丁地不同的路有( )
如图,从甲地到乙地有2条路,从乙地到丁地有3条路;从甲地到丙地有4 条路,从丙地到丁地有2条路,则从甲地到丁地不同的路有( )| A. | 11条 | B. | 14条 | C. | 16条 | D. | 48条 |
14.计算1!+2!+3!+…+100!得到的数,其个位数字是( )
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
 (
( ),则“
),则“ ”是“
”是“ 为纯虚数”的 ( )
为纯虚数”的 ( )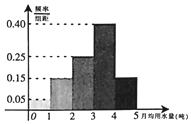 为了解某地区居民用水情况,通过抽样,获得了100位居民每人的月均用水量(单位:吨),将数据按照[0,1),[1,2)…,[4,5]分成5组,制成了如图所示的频率分布直方图.
为了解某地区居民用水情况,通过抽样,获得了100位居民每人的月均用水量(单位:吨),将数据按照[0,1),[1,2)…,[4,5]分成5组,制成了如图所示的频率分布直方图.