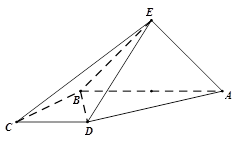
题目内容
如图,三棱锥P-ABC中,PC 平面ABC,PC=AC=2,AB=BC,D是PB上一点,且CD
平面ABC,PC=AC=2,AB=BC,D是PB上一点,且CD 平面PAB
平面PAB
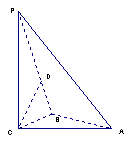
(1)求证:AB 平面PCB;
平面PCB;
(2)求异面直线AP与BC所成角的大小;
(3)求二面角C-PA-B 的大小的余弦值。
 平面ABC,PC=AC=2,AB=BC,D是PB上一点,且CD
平面ABC,PC=AC=2,AB=BC,D是PB上一点,且CD 平面PAB
平面PAB
(1)求证:AB
 平面PCB;
平面PCB;(2)求异面直线AP与BC所成角的大小;
(3)求二面角C-PA-B 的大小的余弦值。
(1)  PC
PC 平面ABC,AB
平面ABC,AB 平面ABC,
平面ABC, PC
PC AB,
AB, CD
CD 平面PAB,AB
平面PAB,AB 平面PAB,
平面PAB,
 CD
CD  AB。又
AB。又 ,
, AB
AB  平面PCB (2)
平面PCB (2)  (3)
(3) 
 PC
PC 平面ABC,AB
平面ABC,AB 平面ABC,
平面ABC, PC
PC AB,
AB, CD
CD 平面PAB,AB
平面PAB,AB 平面PAB,
平面PAB, CD
CD  AB。又
AB。又 ,
, AB
AB  平面PCB (2)
平面PCB (2)  (3)
(3) 
试题分析:(1)
 PC
PC 平面ABC,AB
平面ABC,AB 平面ABC,
平面ABC, PC
PC AB,
AB, CD
CD 平面PAB,AB
平面PAB,AB 平面PAB,
平面PAB,  CD
CD  AB。又
AB。又 ,
, AB
AB  平面PCB
平面PCB(2)由(1)AB
 平面PCB ,
平面PCB , PC=AC=2, 又
PC=AC=2, 又 AB=BC, 可求得BC=
AB=BC, 可求得BC= 
以B为原点,如图建立空间直角坐标系,
则A(0,
 ,0),B(0,0,0), C(
,0),B(0,0,0), C( ,0,0) P(
,0,0) P( ,0,2)
,0,2) =(
=( ,-
,- ,2),
,2),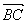 =(
=( ,0,0) 则
,0,0) 则
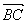 =
=
 +0+0=2
+0+0=2
 异面直线AP与BC所成的角为
异面直线AP与BC所成的角为
(3)设平面PAB的法向量为m=(x,y,z)
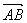 =(0,-
=(0,- ,0),
,0), =(
=( ,
, ,2)
,2)则
 ,即,得m=(
,即,得m=( ,0,-1)设平面PAC的法向量为n=(x,y,z)
,0,-1)设平面PAC的法向量为n=(x,y,z) =(0,0,-2),
=(0,0,-2),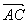 =(
=( ,-
,- ,0),则
,0),则
得n=(1,1,0)cos<m,n>=

 二面角C-PA-B大小的余弦值为
二面角C-PA-B大小的余弦值为
点评:线面垂直的判定定理:一条直线垂直于平面内两条相交直线,则直线垂直于平面,向量法求两直线所成角,二面角时首先找到直线的方向向量和平面的法向量,通过求解向量夹角的到相应角

练习册系列答案
相关题目
 中,
中, ,
, ,
, 为
为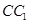 的中点,则异面直线
的中点,则异面直线 与
与 所成角的余弦值为
所成角的余弦值为



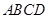 中,
中,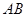 ,
,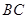 ,
,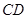 两两互相垂直,且
两两互相垂直,且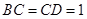 .
.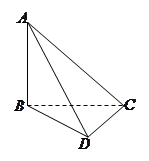
 平面
平面 ;
; 的大小;
的大小; 与平面
与平面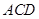 所成的角为
所成的角为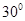 ,求线段
,求线段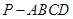 中,侧棱都相等,底面是边长为
中,侧棱都相等,底面是边长为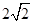 的正方形,底面中心为
的正方形,底面中心为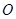 ,以
,以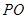 为直径的球经过侧棱中点,则该球的体积为( )
为直径的球经过侧棱中点,则该球的体积为( )
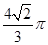


 的正方形E, F分别为PC,BD的中点,侧面PAD⊥底面ABCD,且PA=PD=
的正方形E, F分别为PC,BD的中点,侧面PAD⊥底面ABCD,且PA=PD= AD.
AD.
 平面
平面 ,
, ,
, ,
, ,
, 分别为
分别为 的中点.
的中点.
 平面
平面 ;
; 与平面
与平面 所成角的正弦值.
所成角的正弦值. 中,侧面
中,侧面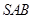 与侧面
与侧面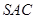 均为等边三角形,
均为等边三角形, 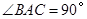 ,
,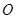 为
为 中点.
中点.
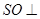 平面
平面 ;
;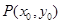
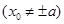 是双曲线
是双曲线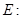
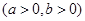 上一点,
上一点,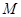 、
、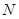 分别是双曲线
分别是双曲线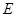 的左、右顶点,直线
的左、右顶点,直线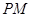 ,
,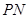 的斜率之积为
的斜率之积为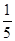 .
.
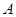 ,
,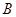 两点,
两点,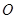 为坐标原点,
为坐标原点,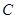 为双曲线上一点,满足
为双曲线上一点,满足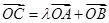 ,求
,求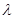 的值.
的值.