题目内容
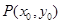
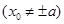 是双曲线
是双曲线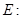
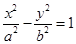
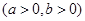 上一点,
上一点,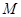 、
、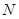 分别是双曲线
分别是双曲线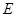 的左、右顶点,直线
的左、右顶点,直线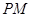 ,
,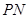 的斜率之积为
的斜率之积为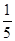 .
.
(1)求双曲线的离心率;
(2)过双曲线
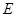 的右焦点且斜率为1的直线交双曲线于
的右焦点且斜率为1的直线交双曲线于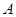 ,
,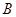 两点,
两点,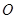 为坐标原点,
为坐标原点,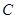 为双曲线上一点,满足
为双曲线上一点,满足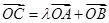 ,求
,求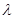 的值.
的值.(1) e=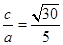 . (2)λ=0或λ=-4.
. (2)λ=0或λ=-4.
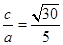 . (2)λ=0或λ=-4.
. (2)λ=0或λ=-4. 试题分析:(1)点P(x0,y0)(x0≠±a)在双曲线
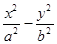 =1上,有
=1上,有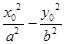 =1, 1分
=1, 1分由题意又有
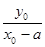 ·
· =
=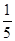 , 2分
, 2分可得a2=5b2,c2=a2+b2=6b2,则e=
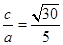 . 4分
. 4分(2)联立
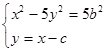 ,得4x2-10cx+35b2=0,设A(x1,y1),B(x2,y2)
,得4x2-10cx+35b2=0,设A(x1,y1),B(x2,y2)则
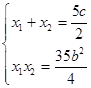 ① 6分
① 6分设
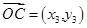 ,
,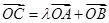 ,即
,即
又C为双曲线上一点,即
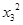 -5
-5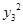 =5b2,有(λx1+x2)2-5(λy1+y2)2=5b2 。7分
=5b2,有(λx1+x2)2-5(λy1+y2)2=5b2 。7分化简得:λ2(
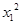 -5
-5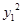 )+(
)+( -5
-5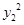 )+2λ(x1x2-5y1y2)=5b2 。9分
)+2λ(x1x2-5y1y2)=5b2 。9分又A(x1,y1),B(x2,y2)在双曲线上,所以
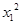 -5
-5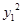 =5b2,
=5b2, -5
-5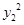 =5b2
=5b2由①式又有x1x2-5y1y2=x1x2-5(x1-c)(x2-c)=-4x1x2+5c(x1+x2)-5c2=10b2
得λ2+4λ=0,解出λ=0或λ=-4. 12分
点评:难题,曲线关系问题,往往通过联立方程组,得到一元二次方程,运用韦达定理。本题利用双曲线的标准方程,确定得到离心率。本题(II)在利用韦达定理的基础上,又利于点在曲线上得到λ的方程,使问题得解。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 平面ABC,PC=AC=2,AB=BC,D是PB上一点,且CD
平面ABC,PC=AC=2,AB=BC,D是PB上一点,且CD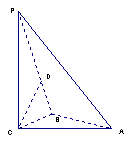
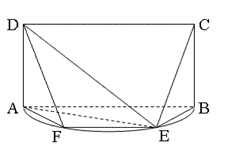
 是以
是以 为直径的半圆上异于
为直径的半圆上异于 、
、 的点,矩形
的点,矩形 所在的平面垂直于该半圆所在的平面,且
所在的平面垂直于该半圆所在的平面,且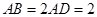 .
.
 ;
; 与半圆弧的另一个交点为
与半圆弧的另一个交点为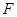 .
. ;
; ,求三棱锥
,求三棱锥 的体积.
的体积. 中,侧棱与底面垂直,
中,侧棱与底面垂直, ,
, ,点
,点 分别为
分别为 和
和 的中点.
的中点.
 ;
; 的正弦值.
的正弦值.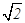 ,
,
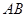 为圆
为圆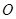 的直径,点
的直径,点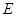 、
、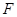 在圆
在圆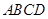 所在的平面和圆
所在的平面和圆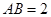 ,
,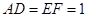 .
.
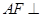 平面
平面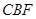 ;
;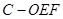 的体积.
的体积.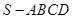 的底面边长为
的底面边长为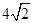 ,高
,高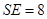 ,点
,点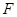 在高
在高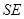 上,且
上,且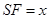 ,记过点
,记过点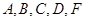 的球的半径为
的球的半径为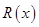 ,则函数
,则函数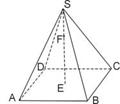
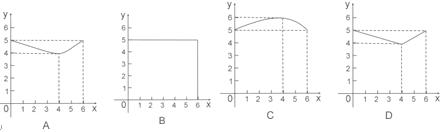
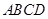 与正三角形
与正三角形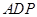 所在的平面相互垂直,且
所在的平面相互垂直,且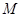 、
、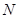
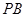 、
、 中点.
中点.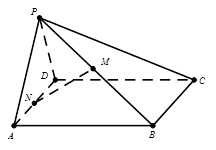
 ;
; 与平面
与平面 所成角的正弦值.
所成角的正弦值.