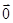题目内容
如图,四棱锥P—ABCD中,底面ABCD是边长为 的正方形E, F分别为PC,BD的中点,侧面PAD⊥底面ABCD,且PA=PD=
的正方形E, F分别为PC,BD的中点,侧面PAD⊥底面ABCD,且PA=PD= AD.
AD.

(Ⅰ)求证:EF//平面PAD;
(Ⅱ)求三棱锥C—PBD的体积.
 的正方形E, F分别为PC,BD的中点,侧面PAD⊥底面ABCD,且PA=PD=
的正方形E, F分别为PC,BD的中点,侧面PAD⊥底面ABCD,且PA=PD= AD.
AD.
(Ⅰ)求证:EF//平面PAD;
(Ⅱ)求三棱锥C—PBD的体积.
(1)对于线面平行的证明,主要是根据线面平行的判定定理,根据EF//PA,来得到证明。
(2)
 PM=
PM=
(2)

 PM=
PM=
试题分析:解:(Ⅰ)证明:连接AC,则F是AC的中点,
E为PC的中点,故在
 CPA中,EF//PA,
CPA中,EF//PA,且PA
 平面PAD,EF
平面PAD,EF 平面PAD,∴EF//平面PAD
平面PAD,∴EF//平面PAD(Ⅱ)取AD的中点M,连接PM,∵PA=PD,∴PM⊥AD,又平面PAD⊥平面ABCD,
平面PAD∩平面ABCD=AD,∴PM⊥平面ABCD.
在直角
 PAM中,求得PM=
PAM中,求得PM= ,∴
,∴
 PM=
PM=
点评:解决的关键是根据线面平行的判定定理来得到证明,同事能结合等体积法来求解几何体的体积,是常用的转换方法,属于基础题。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 表示一条直线,则M内至少有一直线与
表示一条直线,则M内至少有一直线与 中,
中, ,且
,且 ,
, 平面
平面 ,过
,过 作截面分别交
作截面分别交 于
于 ,且二面角
,且二面角 的大小为
的大小为 ,则截面
,则截面 面积的最小值为 .
面积的最小值为 .
 EA=EC=6,M为EC中点,平面BCE⊥平面ACE,AE⊥EB
EA=EC=6,M为EC中点,平面BCE⊥平面ACE,AE⊥EB

 平面ABC,PC=AC=2,AB=BC,D是PB上一点,且CD
平面ABC,PC=AC=2,AB=BC,D是PB上一点,且CD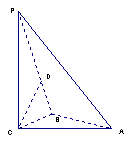
 ABC的边AB,BC,CA的中点,O是△ABC的重心,则
ABC的边AB,BC,CA的中点,O是△ABC的重心,则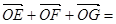 ( )
( )