题目内容
设a,b,c,d正数,且m<
<n,m<
<n,比较m,n,
的大小.
| a |
| b |
| c |
| d |
| a+c |
| b+d |
考点:不等式的基本性质
专题:不等式
分析:根据不等式的性质,不等式的两边同乘一个正数,符号不变,再根据不等式的同向可加性,再不等式每项分别除于b+d,问题得以解决
解答:
解:因为a,b,c,d为正数,m<
<n,m<
<n,
所以bm<a<bn,dm<c<dn,
∴bm+dm<a+c<bn+dn,
∴m(b+d)<a+c<n(b+d).
∴m<
<n
| a |
| b |
| c |
| d |
所以bm<a<bn,dm<c<dn,
∴bm+dm<a+c<bn+dn,
∴m(b+d)<a+c<n(b+d).
∴m<
| a+c |
| b+d |
点评:本题考查了不等式的基本性质,属于基础题

练习册系列答案
相关题目
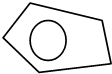 如图,在一个不规则多边形内随机撒入200粒芝麻(芝麻落到任何位置的可能性相等),恰有40粒落入半径为1的圆内,则该多边形的面积约为( )
如图,在一个不规则多边形内随机撒入200粒芝麻(芝麻落到任何位置的可能性相等),恰有40粒落入半径为1的圆内,则该多边形的面积约为( )| A、4π | B、5π | C、6π | D、7π |




