题目内容

已知A（4，-3）、B（2，-1）和直线L：4x+3Y-2=0，求一点P，使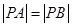，且点P到L的距离等于2

 

【答案】

P（1，-4）和P（，-）

【解析】解：设点P的坐标为（3，-2），kAB==－1，线段的垂直平分线方程为y+2=x-3，即x-y-5=0   点P（a，b）在直线x-y-5=0上，故a-b-5=0

又

又两个式子得：或   

∴所求的点为P（1，-4）和P（，-）

 

练习册系列答案
相关题目
平面向量
a
，
b
，已知
a
=（4，3），2
a
+
b
=（3，18），则
a
，
b
夹角的余弦值等于（　　）
A、
8
65
B、-
8
65
C、
16
65
D、-
16
65
已知A（4，-3），B（-2，6），点P在直线AB上，且|
AB
|=3|
AP
|，则P点的坐标为（　　）
已知A（-4，3），B（5，12），若
AP
=2
PB
，那么点 P的坐标是
（2，9）
（2，9）
．
（2012•包头一模）
a
，
b
为平面向量，已知
a
=（4，3），2
a
+
b
=（3，18），则
a
，
b
夹角的余弦值等于
16
65
16
65
．
已知A（4，3），且P是双曲线x2-y2=2上一点，F2为双曲线的右焦点，则|PA|+|PF2|的最小值是
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网