题目内容
（2012•包头一模）
，
为平面向量，已知
=（4，3），2
+
=（3，18），则
，
夹角的余弦值等于
．
| a |
| b |
| a |
| a |
| b |
| a |
| b |
| 16 |
| 65 |
| 16 |
| 65 |
分析：根据题意，易得
=（-5，12），从而得到向量
、
的数量积和
、
的模，再由两个向量夹角的坐标公式，可算出向量
、
的夹角的余弦值．
| b |
| a |
| b |
| a |
| b |
| a |
| b |
解答：解：∵
=（4，3），2
+
=（3，18），
∴
=（-5，12）
因此，
•
=4×（-5）+3×12=16，|
|=
=5，|
|=
=13
∴
、
的夹角θ满足cosθ=
=
=
故答案为：
| a |
| a |
| b |
∴
| b |
因此，
| a |
| b |
| a |
| 42+32 |
| b |
| (-5)2+122 |
∴
| a |
| b |
| ||||
|
| 16 |
| 5×13 |
| 16 |
| 65 |
故答案为：
| 16 |
| 65 |
点评：本题已知
和2
+
的坐标，求向量
、
的夹角的余弦值．着重考查了数量积表示两个向量的夹角、平面向量模与夹角的公式等知识，属于基础题．
| a |
| a |
| b |
| a |
| b |
练习册系列答案
相关题目
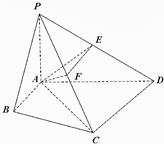（2012•包头一模）在四棱锥P-ABCD中，∠ABC=∠ACD=90°，∠BAC=∠CAD=60°，PA⊥平面ABCD，E为PD的中点，PA=2，AB=1．
（2012•包头一模）函数f（x）=sin（ωx+?）（其中