题目内容
16.已知直线l1:x+ay+3=0与直线l2:x-2y+1=0垂直,则a的值为( )| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | 2 | D. | -2 |
分析 当两条直线垂直时,A1A2+B1B2=0,解方程求出a的值.
解答 解:由题意得:1-2a=0,解得a=$\frac{1}{2}$,
故选:A.
点评 本题考查两直线垂直的条件,体现了转化的数学思想.属于基础题.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目
4.设集合A={a|0<a<1},B={a∈R|ax2+4ax-4<0对任意实数x恒成立},则下列关系成立的是( )
| A. | A?B | B. | B?A | C. | A=B | D. | A∩B=∅ |
11.设集合A={x|0≤x≤3},B={x|x<2},则A∪B=( )
| A. | (-∞,2) | B. | (-∞,3] | C. | [0,2) | D. | [0,3] |
1.已知F1,F2是双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$的左右焦点,过F2作双曲线一条渐近线的垂线,垂足为点A,交另一条渐近线于点B,且$\overrightarrow{A{F_2}}=\frac{1}{3}\overrightarrow{{F_2}B}$,则该双曲线的离心率为( )
| A. | $\frac{{\sqrt{6}}}{2}$ | B. | $\frac{{\sqrt{5}}}{2}$ | C. | $\sqrt{3}$ | D. | 2 |
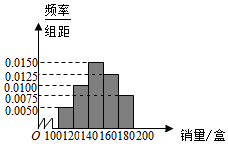 某大学在开学季准备销售一种盒饭进行试创业,在一个开学季内,每售出1盒该盒饭获利润10元,未售出的产品,每盒亏损5元.根据历史资料,得到开学季市场需求量的频率分布直方图,如图所示.该同学为这个开学季购进了150盒该产品,以x(单位:盒,100≤x≤200)表示这个开学季内的市场需求量,y(单位:元)表示这个开学季内经销该产品的利润.
某大学在开学季准备销售一种盒饭进行试创业,在一个开学季内,每售出1盒该盒饭获利润10元,未售出的产品,每盒亏损5元.根据历史资料,得到开学季市场需求量的频率分布直方图,如图所示.该同学为这个开学季购进了150盒该产品,以x(单位:盒,100≤x≤200)表示这个开学季内的市场需求量,y(单位:元)表示这个开学季内经销该产品的利润.