题目内容
设整数 3,集合P
3,集合P {1,2,3,…,n},A,B是P的两个非空子集.记an为所有满足A中的最大数小于B中的最小数的集合对(A,B)的个数.
{1,2,3,…,n},A,B是P的两个非空子集.记an为所有满足A中的最大数小于B中的最小数的集合对(A,B)的个数.
(1)求a3;
(2)求an.
(1)当 3时,P
3时,P {1,2,3 },
{1,2,3 },
其非空子集为:{1},{2},{3},{1,2},{1,3},{2,3},{1,2,3},
则所有满足题意的集合对(A,B)为:({1},{2}),({1},{3}),({2},{3}),
({1},{2,3}),({1,2},{3})共5对,
所以a3 ;
;
(2)设A中的最大数为k,其中 ,整数
,整数 3,
3,
则A中必含元素k,另元素1,2,…,k 可在A中,故A的个数为:
可在A中,故A的个数为:
 ,
,
B中必不含元素1,2,…,k,另元素k 1,k
1,k 2,…,n可在B中,但不能
2,…,n可在B中,但不能
都不在B中,故B的个数为: ,
,
从而集合对(A,B)的个数为
 ,
,
所以an .
.

练习册系列答案
相关题目
 中,“角
中,“角 成等差数列”是“
成等差数列”是“ ”成立的的 条件.
”成立的的 条件. 轴的正半轴为极轴建立极坐标系,两种坐标系取相同的单位长度.已知曲线
轴的正半轴为极轴建立极坐标系,两种坐标系取相同的单位长度.已知曲线 (
( 为参数)和曲线
为参数)和曲线 相交于
相交于 两点,求
两点,求 中点的直角坐标.
中点的直角坐标.

 sinx+
sinx+ cosx的图象上存在两条切线垂直,则a的值是 .
cosx的图象上存在两条切线垂直,则a的值是 .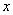 值是 .
值是 .
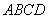 建造市民健身广场,设计时决定保留空地边上的一个水塘(如图中阴影部分),水塘可近似看作一个等腰直角三角形,其中
建造市民健身广场,设计时决定保留空地边上的一个水塘(如图中阴影部分),水塘可近似看作一个等腰直角三角形,其中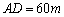 ,
,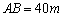 ,且
,且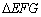 中,
中,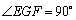 ,经测量得到
,经测量得到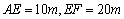 .为保证安全同时考虑美观,健身广场周围准备加设一个保护栏.设计时经过点
.为保证安全同时考虑美观,健身广场周围准备加设一个保护栏.设计时经过点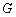 作一条直线交
作一条直线交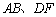 于
于 ,从而得到五边形
,从而得到五边形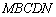 的市民健身广场.
的市民健身广场.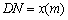 ,试将五边形
,试将五边形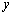 表示为
表示为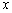 的函数,并注明函数的定义域;
的函数,并注明函数的定义域;