题目内容
如图,正方体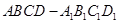 中,点
中,点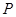 在侧面
在侧面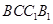 及其边界上运动,并且总是保持
及其边界上运动,并且总是保持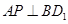 ,则动点
,则动点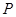 的轨迹是 ( )
的轨迹是 ( )
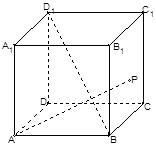
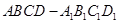 中,点
中,点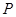 在侧面
在侧面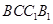 及其边界上运动,并且总是保持
及其边界上运动,并且总是保持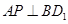 ,则动点
,则动点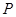 的轨迹是 ( )
的轨迹是 ( )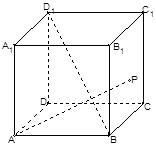
A.线段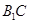 |
B.线段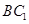 |
C.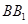 中点与 中点与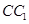 中点连成的线段 中点连成的线段 |
D.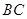 中点与 中点与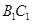 中点连成的线段 中点连成的线段 |
A
试题分析:如下图所示,连接
 、
、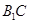 、
、 ,由于四边形
,由于四边形 为正方形,所以
为正方形,所以 ,因为
,因为 平面
平面 ,
, 平面
平面 ,
, ,因为
,因为 ,所以
,所以 平面
平面 ,
, 平面
平面 ,所以
,所以 ,同理可证
,同理可证 ,因为
,因为 ,所以
,所以 平面
平面 ,
,因为
 平面
平面 ,所以
,所以 ,过点
,过点 有且只有一个平面与
有且只有一个平面与 垂直,且过点
垂直,且过点 与
与 垂直的直线都在此平面内,故
垂直的直线都在此平面内,故 平面
平面 ,而平面
,而平面 平面
平面 ,故点
,故点 在侧面
在侧面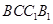 内的轨迹为线段
内的轨迹为线段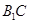 ,故选A.
,故选A.

练习册系列答案
相关题目
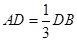 ,点C为圆O上一点,且
,点C为圆O上一点,且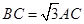 .点P在圆O所在平面上的正投影为点D,PD=DB.
.点P在圆O所在平面上的正投影为点D,PD=DB.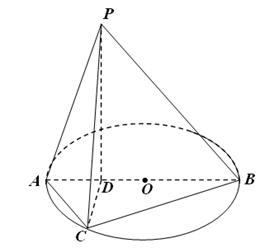
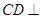 平面
平面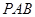 ;
;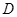 到平面
到平面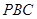 的距离.
的距离.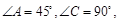
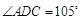 ,
,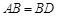 ,现将四边形ABCD沿BD折起,使平面ABD
,现将四边形ABCD沿BD折起,使平面ABD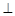 平面BDC,设点F为棱AD的中点.
平面BDC,设点F为棱AD的中点.

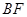 与平面ACD所成角的余弦值.
与平面ACD所成角的余弦值. 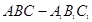 中,
中,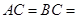
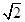 ,且
,且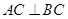 ,点
,点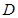 是
是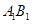 中点.
中点.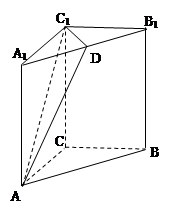
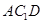 ⊥平面
⊥平面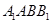 ;
;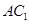 与平面
与平面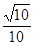 ,
,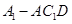 的体积.
的体积.
 ,底面
,底面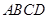 是平行四边形,点
是平行四边形,点 在平面
在平面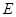 在
在 边上,且
边上,且 ,
,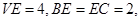
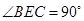 .
.
 是
是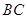 的中点,求异面直线
的中点,求异面直线 与
与 所成角的余弦值;
所成角的余弦值; 在棱
在棱 .求
.求 的值.
的值.
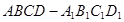 中,
中,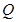 是
是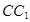 的中点,
的中点,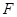 是侧面
是侧面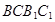 内的动点且
内的动点且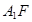 //平面
//平面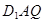 ,则
,则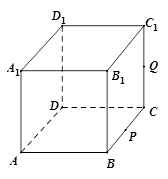
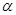 、
、 是两个不同的平面,
是两个不同的平面,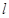 是一条直线,以下命题:
是一条直线,以下命题: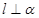 ,
,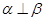 ,则
,则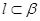 ;②若
;②若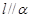 ,
,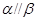 ,则
,则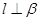 ;④若
;④若