题目内容
如图,已知在侧棱垂直于底面的三棱柱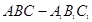 中,
中,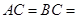
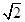 ,且
,且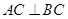 ,点
,点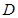 是
是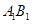 中点.
中点.
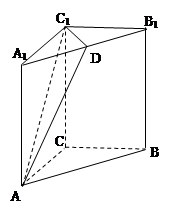
(1)求证:平面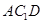 ⊥平面
⊥平面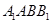 ;
;
(2)若直线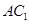 与平面
与平面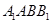 所成角的正弦值为
所成角的正弦值为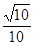 ,
,
求三棱锥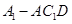 的体积.
的体积.
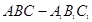 中,
中,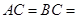
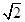 ,且
,且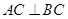 ,点
,点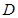 是
是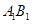 中点.
中点.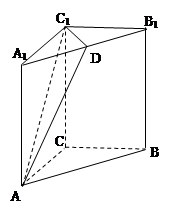
(1)求证:平面
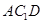 ⊥平面
⊥平面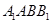 ;
;(2)若直线
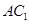 与平面
与平面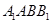 所成角的正弦值为
所成角的正弦值为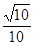 ,
,求三棱锥
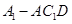 的体积.
的体积.(1)证明详见解析(2)

试题分析:(1)由
 平面
平面 可证
可证
 ,由已知条件可得
,由已知条件可得
 ,,所以在
,,所以在
 平面
平面 ,然后根据平面与平面垂直的判定定理可得平面
,然后根据平面与平面垂直的判定定理可得平面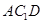 ⊥平面
⊥平面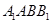 .(2) 先求三角形
.(2) 先求三角形 的面积和
的面积和 的值,然后再根据棱锥的体积公式求解即可.
的值,然后再根据棱锥的体积公式求解即可.试题解析:(1)证明:

 平面
平面 ,
, 平面
平面 ,
,

 ,又
,又
 且点
且点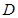 是
是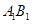 中点.
中点.

 平面
平面 ,又
,又
 平面
平面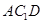 ,
, 平面
平面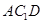 ⊥平面
⊥平面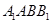 6分
6分(2)由(1)可知
 ,所以AC1与平面A1ABB1所成的角为
,所以AC1与平面A1ABB1所成的角为 ,在
,在 ,由
,由 ,
,


 =
= 12分
12分
练习册系列答案
 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
相关题目
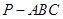 中,
中,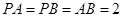 ,
,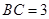 ,
,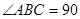 °,平面
°,平面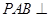 平面
平面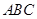 ,
,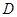 、
、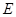 分别为
分别为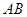 、
、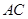 中点.
中点.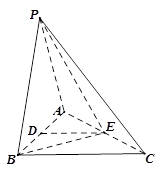
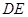 ∥平面
∥平面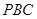 ;
;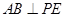 ;
; 的大小.
的大小.
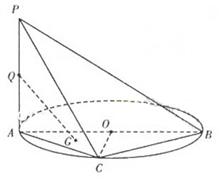


 平面ABCD,且AD= 2PA,E、F、G、H分别是线段PA、PD、CD、BC的中点.
平面ABCD,且AD= 2PA,E、F、G、H分别是线段PA、PD、CD、BC的中点.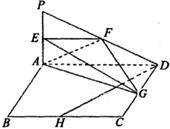
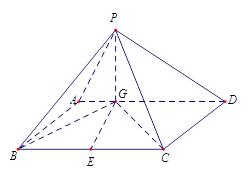
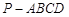 中,底面
中,底面 是平行四边形,
是平行四边形,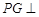 平面
平面 ,垂足为
,垂足为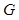 ,
,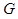 在
在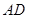 上且
上且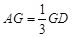 ,
,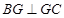 ,
,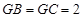 ,
,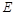 是
是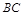 的中点,四面体
的中点,四面体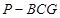 的体积为
的体积为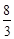 .
.
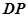 到平面
到平面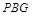 所成角的正弦值;
所成角的正弦值;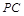 上是否存在一点
上是否存在一点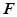 ,使
,使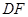
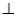
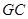 ,若存在,确定点
,若存在,确定点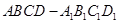 中,点
中,点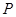 在侧面
在侧面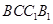 及其边界上运动,并且总是保持
及其边界上运动,并且总是保持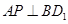 ,则动点
,则动点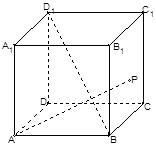
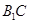
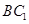
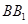 中点与
中点与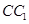 中点连成的线段
中点连成的线段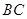 中点与
中点与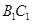 中点连成的线段
中点连成的线段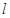 上有无数个点不在平面
上有无数个点不在平面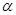 内,则
内,则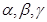 是三个不同的平面,上述命题中真命题的是
是三个不同的平面,上述命题中真命题的是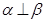 ,
,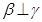 ,则
,则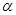 ∥
∥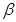 ;
;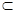
 ,
,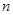 是两条不同直线,
是两条不同直线, ,
, 是两个不同平面,则下列命题错误的是( )
是两个不同平面,则下列命题错误的是( )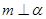 ,
,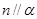 ,则
,则
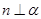 ,
, ,则
,则
 ,则
,则
 ,则
,则