题目内容
 如图,已知三棱柱ABC-A1B1C1中,侧棱垂直于底面,底面△ABC中AC=3,AB=5,BC=4,点D是AB的中点,求证:(1)AC⊥BC1;
如图,已知三棱柱ABC-A1B1C1中,侧棱垂直于底面,底面△ABC中AC=3,AB=5,BC=4,点D是AB的中点,求证:(1)AC⊥BC1;(2)AC1∥平面CDB1.
考点:直线与平面平行的判定,棱柱的结构特征
专题:空间位置关系与距离
分析:运用线面垂直的判定定理和性质定理以及线面平行的判定定理,进行分别证明.
解答:
 证明:(1)在△ABC中,由AC=3,AB=5,BC=4,
证明:(1)在△ABC中,由AC=3,AB=5,BC=4,
∴32+42=52,
∴△ABC为直角三角形,
∴AC⊥BC,
又∵CC1⊥面ABC,
∴CC1⊥AC,CC1∩BC=C,
∴AC⊥面BCC1,
∴AC⊥BC1;
(2)连结B1C交BC1于点E,
则E为BC1的中点,连结DE,
则在△ABC1中,DE∥AC1,
又DE?面CDB1,AC1?面B1CD则AC1∥面B1CD.
 证明:(1)在△ABC中,由AC=3,AB=5,BC=4,
证明:(1)在△ABC中,由AC=3,AB=5,BC=4,∴32+42=52,
∴△ABC为直角三角形,
∴AC⊥BC,
又∵CC1⊥面ABC,
∴CC1⊥AC,CC1∩BC=C,
∴AC⊥面BCC1,
∴AC⊥BC1;
(2)连结B1C交BC1于点E,
则E为BC1的中点,连结DE,
则在△ABC1中,DE∥AC1,
又DE?面CDB1,AC1?面B1CD则AC1∥面B1CD.
点评:本题考查了线面垂直的判定定理和性质定理的运用以及线面平行的判定定理的运用.

练习册系列答案
相关题目
函数f(x)=x-ex在R上的零点个数是( )
| A、0 | B、1 | C、2 | D、3 |
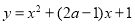 在区间(-∞,2
在区间(-∞,2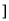 上是减函数,则实数
上是减函数,则实数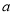 的取值范围是( )
的取值范围是( )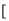 -
-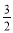 ,+∞) B.(-∞,-
,+∞) B.(-∞,- 与圆
与圆 相外切, 则
相外切, 则 的最大值为 ( )
的最大值为 ( ) B.
B. C.
C. D.
D.
 已知椭圆C:
已知椭圆C: 函数y=Asin(ωx+φ)(A>0,ω>0,0<φ<2π)一个周期的图象如图所示,试确定A、ω、φ的值.
函数y=Asin(ωx+φ)(A>0,ω>0,0<φ<2π)一个周期的图象如图所示,试确定A、ω、φ的值.