题目内容
已知二次函数f(x)在x=
处取得最小值-
(t≠0),且f(1)=0
(1)求f(x)的表达式
(2)若函数f(x)在闭区间[-1,
]上的最小值是-5,求对应的t和x的值.
| t+2 |
| 2 |
| t2 |
| 4 |
(1)求f(x)的表达式
(2)若函数f(x)在闭区间[-1,
| 1 |
| 2 |
考点:二次函数在闭区间上的最值,函数解析式的求解及常用方法
专题:函数的性质及应用
分析:(1)(1)根据条件可设二次函数的顶点式f(x)=a(x-
)2-
,由f(1)=0,可得a,从而求得f(x)表达式.
(2)根据对称轴与区间的位置关系分三种情况进行讨论,求出其最小值,令其等于-5,即可求得t值.
| t+2 |
| 2 |
| t2 |
| 4 |
(2)根据对称轴与区间的位置关系分三种情况进行讨论,求出其最小值,令其等于-5,即可求得t值.
解答:
解:(1)设二次函数f(x)=a(x-
)2-
,
又f(1)=0,所以a(1-
)2-
=0,解得a=1,
所以f(x)=(x-
)2-
(t≠0);
(2)因为f(x)=(x-
)2-
(t≠0);
①当
<-1,即t<-4时,
f(x)min=f(-1)=(-1-
)2-
=-5,解得t=-
;
②当-1≤
≤
,即-4≤t≤-1时,
f(x)min=f(
)=-
=-5,解得t=±2
(舍去);
③当
>
,即t>-1时,
f(x)min=f(
)=(
-
)2-
=-5,解得t=-
(舍去).
综上得,所求的t=-
,x=-1.
| t+2 |
| 2 |
| t2 |
| 4 |
又f(1)=0,所以a(1-
| t+2 |
| 2 |
| t2 |
| 4 |
所以f(x)=(x-
| t+2 |
| 2 |
| t2 |
| 4 |
(2)因为f(x)=(x-
| t+2 |
| 2 |
| t2 |
| 4 |
①当
| t+2 |
| 2 |
f(x)min=f(-1)=(-1-
| t+2 |
| 2 |
| t2 |
| 4 |
| 9 |
| 2 |
②当-1≤
| t+2 |
| 2 |
| 1 |
| 2 |
f(x)min=f(
| t+2 |
| 2 |
| t2 |
| 4 |
| 5 |
③当
| t+2 |
| 2 |
| 1 |
| 2 |
f(x)min=f(
| 1 |
| 2 |
| 1 |
| 2 |
| t+2 |
| 2 |
| t2 |
| 4 |
| 21 |
| 2 |
综上得,所求的t=-
| 9 |
| 2 |
点评:本题考查二次函数在闭区间上最值问题及二次函数解析式的求解,考查分类讨论思想、数形结合思想,属中档题

练习册系列答案
 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
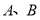 为两个定点,
为两个定点,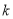 为非零常数,
为非零常数, ,则动点
,则动点 的轨迹为双曲线;
的轨迹为双曲线;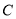 上一定点
上一定点 作圆的动点弦
作圆的动点弦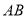 ,
,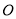 为坐标原点,若
为坐标原点,若 则动点
则动点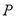 的轨迹为圆;
的轨迹为圆; ,则双曲线
,则双曲线 与
与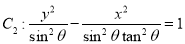 的离心率相同;
的离心率相同;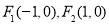 和一动点
和一动点 ,若
,若 ,则点
,则点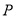 的轨迹关于原点对称.
的轨迹关于原点对称.