题目内容
1．已知数列{an}各项为正数，Sn是其前n项和，且${s_n}=2{n^2}-30n$．求a1及an．分析 Sn=2n2-30n，可得n=1时，a1=S1．n≥2时，an=Sn-Sn-1．
解答 解：∵Sn=2n2-30n，
∴n=1时，a1=S1=2-30=-28．
n≥2时，an=Sn-Sn-1=2n2-30n-[2（n-1）2-30（n-1）]=4n-32，（n=1时也成立）．
∴a1=-28；
∴an=4n-32
点评 本题考查了数列递推关系、数列通项公式，考查了推理能力与计算能力，属于中档题．
练习册系列答案
相关题目
12．某学校为了制定治理学校门口上学、放学期间家长接送孩子乱停车现象的措施，对全校学生家长进行了问卷调查．根据从其中随机抽取的50份调查问卷，得到了如下的列联表：
已知在抽取的50份调查问卷中随机抽取一份，抽到不同意限定区域停车问卷的概率为$\frac{2}{5}$．
（Ⅰ）请将上面的列联表补充完整；
（Ⅱ）是否有99.5%的把握认为是否同意限定区域停车与家长的性别有关？请说明理由；
（Ⅲ）学校计划在同意限定区域停车的家长中，按照性别分层抽样选取9人，在上学、放学期间在学校门口维持秩序．已知在抽取的男性家长中，恰有3位日常开车接送孩子．现从抽取的男性家长中再选取2人召开座谈会，求这两人中至少有一人日常开车接送孩子的概率．
附临界值表及参考公式：
${K^2}=\frac{{n{{（{ad-bc}）}^2}}}{{（{a+b}）（{c+d}）（{a+c}）（{b+d}）}}$，其中n=a+b+c+d．
| 同意限定区域停车 | 不同意限定区域停车 | 合计 | |
| 男生 | 5 | ||
| 女生 | 10 | ||
| 合计 | 50 |
（Ⅰ）请将上面的列联表补充完整；
（Ⅱ）是否有99.5%的把握认为是否同意限定区域停车与家长的性别有关？请说明理由；
（Ⅲ）学校计划在同意限定区域停车的家长中，按照性别分层抽样选取9人，在上学、放学期间在学校门口维持秩序．已知在抽取的男性家长中，恰有3位日常开车接送孩子．现从抽取的男性家长中再选取2人召开座谈会，求这两人中至少有一人日常开车接送孩子的概率．
附临界值表及参考公式：
| P（K2≥k） | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
9．△ABC中，角A，B，C所对的边分别是a，b，c，若角A，B，C依次成等差数列，且$a=1，c=\sqrt{3}$，则S△ABC等于（ ）
| A． | $\sqrt{2}$ | B． | $\sqrt{3}$ | C． | $\frac{{\sqrt{3}}}{2}$ | D． | $\frac{3}{4}$ |
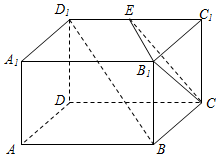已知长方体AC1中，AD=AB=2，AA1=1，E为D1C1的中点，如图所示．