题目内容
7.△ABC的内角A,B,C的对边分别为a、b、c,a=$\sqrt{2}$,b=$\sqrt{3}$,B=60°,那么角A等于( )| A. | 30° | B. | 45° | C. | 135°或45° | D. | 135° |
分析 由已知及正弦定理可解得:sinA=$\frac{\sqrt{2}}{2}$,从而A=45°或135°,由a<b从而确定A=45°.
解答 解:由正弦定理知:$\frac{a}{sinA}=\frac{b}{sinB}$,
∵a=$\sqrt{2}$,b=$\sqrt{3}$,∠B=60°,代入上式,
∴$\frac{\sqrt{2}}{sinA}=\frac{\sqrt{3}}{sin60°}$,故可解得:sinA=$\frac{\sqrt{2}}{2}$,从而A=45°或135°,
∵a<b,
∴A<B,
∴A=45°.
故选:B.
点评 本题主要考查了正弦定理的应用,属于基本知识的考查.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
17.等差数列{an}中,a1=2016,前n项和为Sn,若$\frac{{S}_{12}}{12}$-$\frac{{S}_{10}}{10}$=-2,则S2016=( )
| A. | 2014 | B. | 2015 | C. | 2016 | D. | 2017 |
18.已知函数f(x)是定义在R上的奇函数,f(2)=0,当x>0时,有$\frac{xf'(x)-f(x)}{x^2}>0$成立,则不等式x2f(x)>0的解集是( )
| A. | (-2,0)∪(2,+∞) | B. | (-2,0)∪(0,2) | C. | (2,+∞) | D. | (-∞,-2)∪(2,+∞) |
15.若A={x|x+1>0},B={x|x-3<0},则A∩B等于( )
| A. | {x|x>-1} | B. | {x|x<3} | C. | {x|-1<x<3} | D. | {x|1<x<3} |
2.已知函数f(x)=Acos(ωx+φ)(A>0,ω>0)的图象与直线y=m(-A<m<0)的三个相邻交点的横坐标分别是3,5,9,则f(x)的单调递增区间是( )
| A. | [6kπ+1,6kπ+4],k∈Z | B. | [6k-2,6k+1],k∈Z | C. | [6k+1,6k+4],k∈Z | D. | [6kπ-2,6kπ+1],k∈Z |
17.已知数列{an}是公差大于0的等差数列,且满足a1+a5=4,a2a4=-5,则数列{an}的前10项的和等于( )
| A. | 23 | B. | 95 | C. | 135 | D. | 138 |
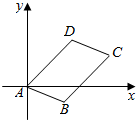 如图,已知平行四边形ABCD的三个顶点的坐标分别为A(0,0),B(2,-1),C(4,2).
如图,已知平行四边形ABCD的三个顶点的坐标分别为A(0,0),B(2,-1),C(4,2).