Question

函数f(x)=

1

x

-lnx的零点个数为

1

．

Answer 1

分析：将零点个数问题转化成函数y=lnx的图象与函数y=

1

x

的图象的交点个数问题，利用图象，即可得到函数数f(x)=

1

x

-lnx的零点个数．

解答：解：f(x)=

1

x

-lnx的零点个数即为函数y=lnx的图象与函数y=

1

x

的图象的交点个数，
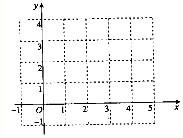
在同一直角坐标系内，做出y=lnx与y=

1

x

的图象，如图所示，
根据图象，可以得到，函数y=lnx的图象与函数y=

1

x

的图象的有且只有一个交点，
∴函数f(x)=

1

x

-lnx的零点个数为1个．
故答案为：1．

点评：本题考查了函数的零点问题，函数的零点等价于对应方程的根，等价于函数的图象与x轴交点的横坐标，解题时要注意根据题意合理的选择转化．运用了数形结合的数学思想方法．属于中档题．