题目内容
如图,四棱柱ABCD-A1B1C1D1的底面ABCD是正方形,O是底面中心,A1O⊥底面ABCD,AB=AA1=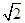 .
.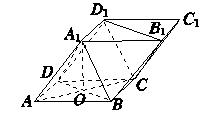
(1)证明:平面A1BD∥平面CD1B1;
(2)求三棱柱ABD-A1B1D1的体积.
(1)证明见解析;(2)1.
解析试题分析:(1)设 线段的中点为
线段的中点为 ,易得四边形
,易得四边形 为平行四边形,得
为平行四边形,得 ,又
,又 ,
, ,
, ,所以平面
,所以平面 平面
平面 ;
;
(2)因为 平面
平面 ,所以
,所以 是三棱柱
是三棱柱 的高,所以三棱柱
的高,所以三棱柱 的体积
的体积 ,通过计算即可得出三棱柱
,通过计算即可得出三棱柱 的体积
的体积 .
.
试题解析:(1) 设 线段的中点为
线段的中点为 .
. 和
和 是棱柱
是棱柱 的对应棱
的对应棱
同理, 和
和 是棱柱
是棱柱 的对应棱
的对应棱
 且
且
 且
且
 四边形
四边形 为平行四边形
为平行四边形
 ,
, ,
,
 平面
平面 平面
平面
(2)
 平面
平面
 是三棱柱
是三棱柱 的高
的高
在正方形 中,
中, .在
.在 中,
中, ,
, 三棱柱
三棱柱 的体积
的体积 .
.
所以,三棱柱 的体积
的体积 .
.
考点:1.面面平行的判定定理;2.棱柱的体积.

练习册系列答案
 53天天练系列答案
53天天练系列答案
相关题目
 为正方形,平面
为正方形,平面 为等腰梯形,
为等腰梯形, ,
,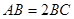 ,
, ,
, .
.
 平面
平面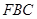 ;
; 与平面
与平面 所成角的正弦值.
所成角的正弦值. 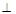 平面CDE,AE=3.
平面CDE,AE=3.
 为
为 的中点,求证:
的中点,求证: 平面
平面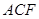 ;
;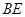 与平面
与平面 所成角的正弦值.
所成角的正弦值.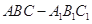 中,
中,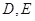 分别是
分别是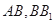 的中点,
的中点, .
.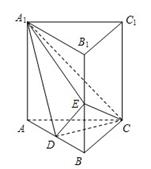
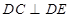 ;
;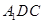 所成角的正弦值.
所成角的正弦值.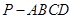 中,底面
中,底面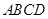 为菱形,
为菱形,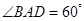 ,
,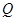 为
为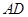 的中点.
的中点.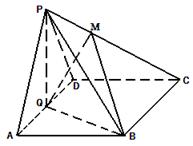
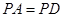 ,求证:平面
,求证:平面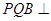 平面
平面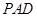 ;
;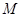 在线段
在线段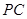 上,
上,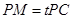 ,试确定
,试确定 的值,使
的值,使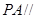 平面
平面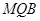 .
.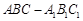 中,
中,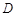 、
、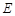 分别是棱
分别是棱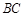 、
、 的中点,点
的中点,点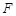 在棱
在棱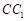 上,已知
上,已知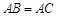 ,
,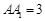 ,
,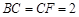 .
.
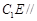 平面
平面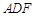 ;
;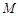 在棱
在棱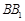 上,当
上,当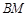 为何值时,平面
为何值时,平面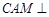 平面
平面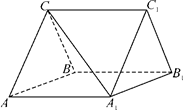
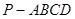 中,底面
中,底面 是个边长为
是个边长为 的正方形,侧棱
的正方形,侧棱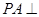 底面
底面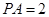 ,
,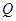 是
是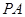 的中点.
的中点.
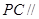 平面
平面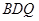 ;
; 的体积.
的体积.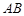 是圆的直径,
是圆的直径,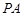 垂直于圆所在的平面,
垂直于圆所在的平面, 是圆上的点.
是圆上的点.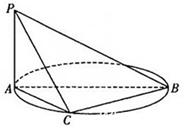
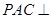 平面
平面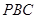 ;
; ,求二面角
,求二面角 的余弦值.
的余弦值.