题目内容
7.用反证法证明:已知0<a<1,0<b<1,0<c<1.求证:(1-a)b,(1-b)c,(1-c)a中至少有一个不大于$\frac{1}{4}$.
分析 首先根据题意,通过反证法假设假设(1-a)b,(1-b)c,(1-c)a中都大于$\frac{1}{4}$,得出:$\sqrt{(1-a)b}$+$\sqrt{(1-b)c}$+$\sqrt{(1-c)a}$>$\frac{3}{2}$;然后根据基本不等式,得出加$\sqrt{(1-a)b}$+$\sqrt{(1-b)c}$+$\sqrt{(1-c)a}$≤$\frac{3}{2}$,相互矛盾,即可证明.
解答 证明:假设(1-a)b,(1-b)c,(1-c)a中都大于$\frac{1}{4}$,
∴(1-a)b>$\frac{1}{4}$,(1-b)c>$\frac{1}{4}$,(1-c)a>$\frac{1}{4}$,
即$\sqrt{(1-a)b}$>$\frac{1}{2}$ ①$\sqrt{(1-b)c}$>$\frac{1}{2}$②$\sqrt{(1-c)a}$>$\frac{1}{2}$③
①②③相加:$\sqrt{(1-a)b}$+$\sqrt{(1-b)c}$+$\sqrt{(1-c)a}$>$\frac{3}{2}$
由基本不等式得$\sqrt{(1-a)b}$≤$\frac{1-a+b}{2}$④,$\sqrt{(1-b)c}$$≤\frac{1-b+c}{2}$⑤,$\sqrt{(1-c)a}$≤$\frac{1-c+a}{2}$⑥
④⑤⑥三式相加 $\sqrt{(1-a)b}$+$\sqrt{(1-b)c}$+$\sqrt{(1-c)a}$≤$\frac{3}{2}$
与$\sqrt{(1-a)b}$+$\sqrt{(1-b)c}$+$\sqrt{(1-c)a}$>$\frac{3}{2}$矛盾.
∴假设不成立,
∴(1-a)b,(1-b)c,(1-c)a中至少有一个不大于$\frac{1}{4}$.
点评 本题考查反证法的应用,涉及不等式的证明与基本不等式的应用,属于中档题.

 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案| A. | 1 | B. | -1 | C. | 2+$\sqrt{3}$ | D. | 2-$\sqrt{3}$ |
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
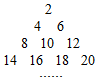 将正偶数排列如图,其中第i行和第j列的数表示为aij=(i,j∈N+),例如a43=18,若aij=2016,则i+j=63.
将正偶数排列如图,其中第i行和第j列的数表示为aij=(i,j∈N+),例如a43=18,若aij=2016,则i+j=63.