题目内容
设集合M={x|0≤x≤2}，集合N={x|x2-x-2＜0}，则M∩N=（ ）
| A、{x|0＜x＜2} |
| B、{x|0≤x＜2} |
| C、{x|0≤x≤2} |
| D、{x0＜x≤2} |
考点：交集及其运算
专题：集合
分析：利用交集定义和不等式性质求解．
解答：
解：∵集合M={x|0≤x≤2}，集合N={x|x2-x-2＜0}={x|-1＜x＜2}，
∴M∩N={x|0≤x＜2}．
故选：B．
∴M∩N={x|0≤x＜2}．
故选：B．
点评：本题考查交集的求法，是基础题，解题时要认真审题，注意不等式性质的合理运用．
练习册系列答案
小学课时特训系列答案
相关题目
已知双曲线的
-
=1的右焦点坐标为（
，0），则该双曲线的渐近线方程为（ ）
| x2 |
| 9 |
| y2 |
| b2 |
| 13 |
A、y=±
| ||
B、y=±
| ||
C、y=±
| ||
D、y=±
|
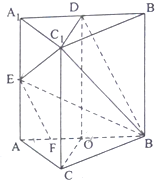在三棱柱ABC-A1B1C1中，AB=BC=CA=AA1，侧棱AA1⊥平面ABC，O、D、E分别是棱AB、A1B1、AA1的中点，点F在棱AB上，且AF=
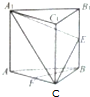如图，在正三棱柱ABC-A1B1C1中，E，F分别为BB1，AC的中点．
如图：程序输出的结果S=132，则判断框中应填（ ）
| A、i≥10？ |
| B、i≤10？ |
| C、i≥11？ |
| D、i≥12？ |