题目内容
14.已知等差数列{an}的前n项和为Sn,若a2=4,S4=22,an=28,则n=( )| A. | 3 | B. | 7 | C. | 9 | D. | 10 |
分析 利用等差数列的通项公式与求和公式即可得出.
解答 解:设等差数列{an}的公差为d,∵a2=4,S4=22,
∴a1+d=4,4a1+$\frac{4×3}{2}$d=22,
解得a1=1,d=3.
∴an=28=1+3(n-1),则n=10.
故选:D.
点评 本题考查了等差数列的通项公式与求和公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
2.如图,△A'B'C'是△ABC的直观图,其中A'B'=A'C',那么△ABC是( )
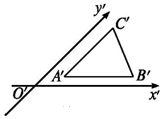

| A. | 等腰三角形 | B. | 直角三角形 | C. | 等腰直角三角形 | D. | 钝角三角形 |
3.已知集合A={1,2,3,4,5,6},B={3,4,5,6,7,8},在集合A∪B中任取一个元素,则该元素是集合A∩B中的元素的概率为( )
| A. | $\frac{1}{6}$ | B. | $\frac{3}{7}$ | C. | $\frac{5}{8}$ | D. | $\frac{1}{2}$ |
4.在△ABC中,角A,B,C所对的边分别是a,b,c,若sinC+sin(B-A)=2sin2A,且 c=2,$∠C=\frac{π}{3}$,则△ABC的面积为( )
| A. | $\frac{{2\sqrt{3}}}{3}$ | B. | $\sqrt{3}$ | C. | $\frac{{4\sqrt{3}}}{3}$ | D. | $\frac{{5\sqrt{3}}}{3}$ |
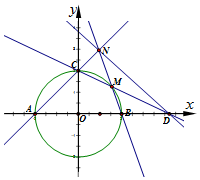 如图,圆O:x2+y2=4与坐标轴交于点A,B,C.设点M是圆上任意一点(不在坐标轴上),直线CM交x轴于点D,直线BM交直线AC于点N.
如图,圆O:x2+y2=4与坐标轴交于点A,B,C.设点M是圆上任意一点(不在坐标轴上),直线CM交x轴于点D,直线BM交直线AC于点N.