题目内容
已知正数a, b, c满足a+b 2c.
2c.
求证: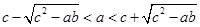 .
.
 2c.
2c.求证:
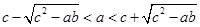 .
.见解析。
将所给不等式分为两个部分:
先证明 <a
<a
要证 <a
<a
即证c-a<
当c-a<0时不等式恒成立,当c-a≥0时,不等式两边平方化简得a(a+b)<2ac
因为a是正数,即证a+b<2c,由已知条件可得,所以 <a。
<a。
同理可证a<c+
先证明
 <a
<a要证
 <a
<a即证c-a<

当c-a<0时不等式恒成立,当c-a≥0时,不等式两边平方化简得a(a+b)<2ac
因为a是正数,即证a+b<2c,由已知条件可得,所以
 <a。
<a。同理可证a<c+


练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
 为正数,求证:
为正数,求证: .
. ,
, ,
, 成等差数列.(1)比较
成等差数列.(1)比较 与
与 的大小,并证明你的结论;(2)求证B不可能是钝角
的大小,并证明你的结论;(2)求证B不可能是钝角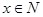 满足
满足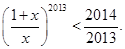 数列
数列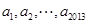 是公差为
是公差为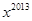 ,首项
,首项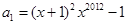 的等差数列; 数列
的等差数列; 数列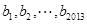 是公比为
是公比为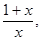 首项
首项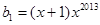 的等比数列,求证:
的等比数列,求证: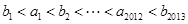 。
。 .
.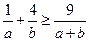 .
.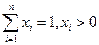 ,求证:
,求证: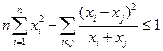 。
。 ,求证:
,求证: