题目内容
6．设i为虚数单位，已知${z_1}=\frac{1-i}{1+i}，{z_2}=-\frac{1}{2}+\frac{{\sqrt{3}}}{2}i$，则|z1|，|z2|的大小关系是（ ）| A． | |z1|＜|z2| | B． | |z1|=|z2| | C． | |z1|＞|z2| | D． | 无法比较 |
分析 利用复数的运算法则分别化简z1，z2，再利用模的计算公式即可得出．
解答 解：z1=$\frac{1-i}{1+i}$=$\frac{（1-i）^{2}}{（1+i）（1-i）}$=$\frac{-2i}{2}$=-i，
∴|z1|=1．
∵${z}_{2}=-\frac{1}{2}+\frac{\sqrt{3}}{2}i$，
∴|z2|=$\sqrt{（-\frac{1}{2}）^{2}+（\frac{\sqrt{3}}{2}）^{2}}$=1，
则|z1|=|z2|．
故选：B．
点评 本题考查了复数的运算法则、模的计算公式，考查了推理能力与计算能力，属于基础题．
练习册系列答案
暑假作业海燕出版社系列答案
相关题目
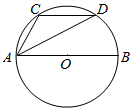如图，AB是⊙O的直径，点C，D是半圆弧AB的三等分点，若$\overrightarrow{AB}$=$\overrightarrow{a}$，$\overrightarrow{AC}$=$\overrightarrow{b}$，则$\overrightarrow{AD}$=$\frac{1}{2}$$\overrightarrow{a}$+$\overrightarrow{b}$．（用a，b表示）
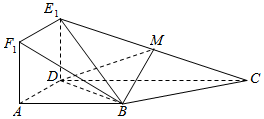19、如图，在直角梯形ABCD中，AB∥CD，且AB=AD=2，CD=4，四边形ADE1F1是正方形，且平面ADE1F1⊥平面ABCD，M是E1C的中点．