题目内容
15.已知四边形ABCD满足|AB|=|AD|,|CD|=$\sqrt{3}$且∠BAD=60°,$\overrightarrow{AC}$-$\overrightarrow{AB}$=$\frac{1}{2}$$\overrightarrow{AD}$,那么四边形ABCD的面积为$\frac{3\sqrt{3}}{2}$.分析 由题意作图辅助,从而可判断四边形为直角梯形,从而求其面积.
解答 解:由题意作图如右图,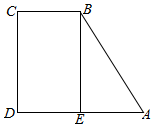
∵$\overrightarrow{AC}$-$\overrightarrow{AB}$=$\overrightarrow{BC}$=$\frac{1}{2}$$\overrightarrow{AD}$,
∴BC∥AD且|BC|=$\frac{1}{2}$|AD|,
又∵|AB|=|AD|,且∠BAD=60°,
∴|AE|=$\frac{1}{2}$|AB|=$\frac{1}{2}$|AD|,
∴|BC|=|DE|,
∴BCDE是平行四边形,
∴CD∥BE,
∴DC⊥AD,
∵|CD|=$\sqrt{3}$,
∴|AB|=|AD|=2,
∴S=$\frac{1+2}{2}$$\sqrt{3}$=$\frac{3\sqrt{3}}{2}$,
故答案为:$\frac{3\sqrt{3}}{2}$.
点评 本题考查了学生的作图能力及数形结合的思想应用,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.设i为虚数单位,已知${z_1}=\frac{1-i}{1+i},{z_2}=-\frac{1}{2}+\frac{{\sqrt{3}}}{2}i$,则|z1|,|z2|的大小关系是( )
| A. | |z1|<|z2| | B. | |z1|=|z2| | C. | |z1|>|z2| | D. | 无法比较 |
3.若x,y满足不等式组$\left\{\begin{array}{l}y-2≥0\\ x-y+1≥0\\ x+y-5≤0\end{array}\right.$,则$\frac{y}{x}$的最大值是( )
| A. | $\frac{3}{2}$ | B. | 1 | C. | 2 | D. | 3 |
20.已知F1,F2分别是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a,b>0)的左.右焦点,且|F1F2|=2,若P是该双曲线右支上的一点,且满足|PF1|=2|PF2|,则△PF1F2面积的最大值是( )
| A. | 2 | B. | $\frac{5}{3}$ | C. | $\frac{4}{3}$ | D. | 1 |
4.根据如样本数据:
得到的回归直线方程为$\widehat{y}$=10.5x+a,据此模型来预测当x=20时,y的值为( )
| x | 2 | 4 | 5 | 6 | 8 |
| y | 20 | 40 | 60 | 70 | 80 |
| A. | 210 | B. | 210.5 | C. | 211.5 | D. | 212.5 |

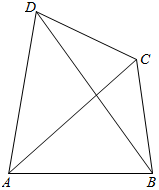 如图,平面四边形ABCD中,AB=$\sqrt{5}$,AD=2$\sqrt{2}$,CD=$\sqrt{3}$,∠CBD=30°,∠BCD=120°,求
如图,平面四边形ABCD中,AB=$\sqrt{5}$,AD=2$\sqrt{2}$,CD=$\sqrt{3}$,∠CBD=30°,∠BCD=120°,求