题目内容
【题目】已知数列{an}的各项均为正数，其前n项和为Sn ， 且an2+an=2Sn ， n∈N* ．
（1）求a1及an；
（2）求满足Sn＞210时n的最小值；
（3）令bn=4 
，证明：对一切正整数n，都有 
+ 
+ 
++ 
＜ 
．
【答案】
（1）解：∵数列{an}的各项均为正数，其前n项和为Sn，且an2+an=2Sn，n∈N*．
∴当n=1时， 
，且a1＞0，解得a1=1，
∵an2+an=2Sn，①，∴ 
，②
①﹣②，得： 
，
整理，得：（an+an﹣1）（an﹣an﹣1﹣1）=0，
∵an＞0，∴an﹣an﹣1=1，
∴数列{an}是首项和公差都为1的等差数列，
∴an=n．
（2）解：∵数列{an}是首项和公差都为1的等差数列，an=n．
∴Sn= 
，
∵Sn＞210，∴ 
，
整理，得n2+n﹣420＞0，解得n＞20（n＜﹣21舍），
∴满足Sn＞210时n的最小值是21．
（3）证明：由题意得 
，则 
，
∴数列{ 
}是首项和公比都是 
的等比数列，
∴ 
+ 
+ 
++ = 
= 
．
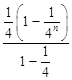故对一切正整数n，都有 + + ++ ＜ 
．
【解析】（1）当n=1时， 
，由此能求出a1=1，由an2+an=2Sn，得 
，从而（an+an﹣1）（an﹣an﹣1﹣1）=0，进而数列{an}是首项和公差都为1的等差数列，由此能求出an=n．（2）求出Sn= 
，由此能求出满足Sn＞210时n的最小值．（3）由题意得 
，从而数列{ 
}是首项和公比都是 
的等比数列，由此能证明对一切正整数n，都有 
+ 
+ 
++ ＜ 
．
【考点精析】本题主要考查了数列的前n项和的相关知识点，需要掌握数列{an}的前n项和sn与通项an的关系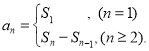
才能正确解答此题．
