Question

【题目】如图多面体ABCD中，面ABCD为正方形，棱长AB=2，AE=3，DE= ，二面角E﹣AD﹣C的余弦值为 ，且EF∥BD．
（1）证明：面ABCD⊥面EDC；
（2）若直线AF与平面ABCD所成角的正弦值为 ，求二面角AF﹣E﹣DC的余弦值．

Answer 1

【答案】
（1）证明：∵AB=2，AE=3， ∴AD2+DE2=AE2∴AD⊥DE

又ABCD为正方形，∴AD⊥DC，

从而AD⊥平面EDC，

于是面ABCD⊥面EDC．

（2）解：由（1）知AD⊥DE，AD⊥DC，

∴∠EDC是二面角E﹣AD﹣C的平面角．

作EO⊥DC交DC于O，则AO=DEcos∠EDO=1，

且EO⊥面ABCD．取AB中点M，则OM⊥DC．

以O为坐标原点， 方向为x，y，z轴正方向建立直角坐标系O﹣xyz．

于是，E（0，0，2），D（0，﹣1，0），B（2，1，0），A（2，﹣1，0）；

得 ， ， ；

∴ ，

又面ABCD的一个法向量为： =（0，0，1），

设直线AF与平面ABCD所成角为θ，

则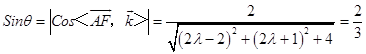

得λ=0（舍去）或 ，

∴ ，

设面AEF的法向量为 ，则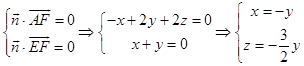

取y=2，∴ ；

又面EDC的一个法向量为 ，

∴

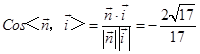
又二面角AF﹣E﹣DC为锐角，所以其余弦值为 ．

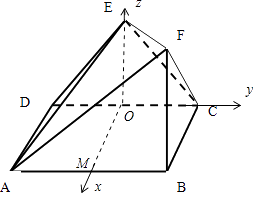
【解析】（1）通过证明AD⊥DE，AD⊥DC，推出AD⊥平面EDC，得到面ABCD⊥面EDC．（2）说明∠EDC是二面角E﹣AD﹣C的平面角．以O为坐标原点， 方向为x，y，z轴正方向建立直角坐标系O﹣xyz．求出相关点的坐标，ABCD的一个法向量为： =（0，0，1），设直线AF与平面ABCD所成角为θ，利用向量的数量积求解即可．求出面AEF的法向量，面EDC的一个法向量，利用空间向量的数量积求解二面角AF﹣E﹣DC的余弦值．
【考点精析】认真审题，首先需要了解平面与平面垂直的判定(一个平面过另一个平面的垂线，则这两个平面垂直)．