题目内容
4.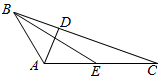 如图所示,在三角形ABC中,AD⊥BC,AD=1,BC=4,点E为AC的中点,$\overrightarrow{DC}•\overrightarrow{BE}$=$\frac{15}{2}$,则AB的长度为( )
如图所示,在三角形ABC中,AD⊥BC,AD=1,BC=4,点E为AC的中点,$\overrightarrow{DC}•\overrightarrow{BE}$=$\frac{15}{2}$,则AB的长度为( )| A. | 2 | B. | $\frac{3}{2}$ | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |
分析 可以D为坐标原点,BC,AD所在直线分别为x轴,y轴,建立平面直角坐标系,并设BD=x,从而CD=4-x,这样便可写出图形上各点的坐标,从而可求出向量$\overrightarrow{DC},\overrightarrow{BE}$的坐标,根据$\overrightarrow{DC}•\overrightarrow{BE}=\frac{15}{2}$进行向量数量积的坐标运算便可建立关于x的方程,解出x,从而得出点B的坐标,从而便可得出AB的长度.
解答 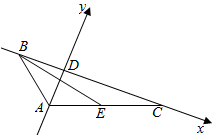 解:以D为原点,分别以BC,AD所在直线为x,y轴,建立如图所示平面直角坐标系,设BD=x,CD=4-x,则:
解:以D为原点,分别以BC,AD所在直线为x,y轴,建立如图所示平面直角坐标系,设BD=x,CD=4-x,则:
D(0,0),A(0,-1),B(-x,0),C(4-x,0),E($\frac{4-x}{2},-\frac{1}{2}$);
∴$\overrightarrow{DC}=(4-x,0),\overrightarrow{BE}=(\frac{4+x}{2},-\frac{1}{2})$;
∴$\overrightarrow{DC}•\overrightarrow{BE}=\frac{16-{x}^{2}}{2}+0=\frac{15}{2}$;
∵x>0,∴解得x=1;
∴B(-1,0),又A(0,-1);
∴$|AB|=\sqrt{1+1}=\sqrt{2}$.
故选:C.
点评 考查通过建立平面直角坐标系,利用向量的坐标解决向量问题的方法,能求平面上点的坐标,根据点的坐标可求向量的坐标,以及向量数量积的坐标运算,两点间的距离公式.

练习册系列答案
相关题目
12.已知实数x,y满足$\left\{\begin{array}{l}{x≥1}\\{x+y≤5}\\{2x-y≤2}\end{array}\right.$若z=y+mx有最大值12,则实数m的取值为( )
| A. | -4 | B. | -8 | C. | 8 | D. | 4 |
19.设a1,a2,…a9成等差数列,若$\sum_{k=1}^{9}{a}_{k}=0,\sum_{k=1}^{9}{a}_{k}^{2}=15$,且a1<a2,则a9=( )
| A. | 2 | B. | $\frac{3}{2}$ | C. | 1 | D. | $\frac{3}{4}$ |
19.函数y=sin24x是( )
| A. | 最小正周期为$\frac{π}{4}$的奇函数 | B. | 最小正周期为π的奇函数 | ||
| C. | 最小正周期为$\frac{π}{4}$的偶函数 | D. | 最小正周期为π的偶函数 |