题目内容
19．设a1，a2，…a9成等差数列，若$\sum_{k=1}^{9}{a}_{k}=0，\sum_{k=1}^{9}{a}_{k}^{2}=15$，且a1＜a2，则a9=（ ）| A． | 2 | B． | $\frac{3}{2}$ | C． | 1 | D． | $\frac{3}{4}$ |
分析 设此等差数列的公差为d，由于$\sum_{k=1}^{9}{a}_{k}=0，\sum_{k=1}^{9}{a}_{k}^{2}=15$，且a1＜a2，可得d＞0，9a5=0，$（{a}_{5}-4d）^{2}$+$（{a}_{5}-3d）^{2}$+…+${a}_{5}^{2}$+$（{a}_{5}+d）^{2}$+…+$（{a}_{5}+4d）^{2}$=15，即$9{a}_{5}^{2}$+60d2=15，化简解出即可得出．
解答 解：设此等差数列的公差为d，∵$\sum_{k=1}^{9}{a}_{k}=0，\sum_{k=1}^{9}{a}_{k}^{2}=15$，且a1＜a2，
∴d＞0，9a5=0，$（{a}_{5}-4d）^{2}$+$（{a}_{5}-3d）^{2}$+…+${a}_{5}^{2}$+$（{a}_{5}+d）^{2}$+…+$（{a}_{5}+4d）^{2}$=15，即$9{a}_{5}^{2}$+60d2=15，
解得a5=0，d=$\frac{1}{2}$．
则a9=${a}_{5}+\frac{1}{2}（9-5）$=2．
故选：A．
点评 本题考查了等差数列的通项公式及其前n项和公式、数列的单调性，考查了推理能力与计算能力，属于中档题．
练习册系列答案
相关题目
10．若函数f（x）同时满足以下三个性质；①f（x）的最小正周期为π；②对任意的x∈R，都有f（x-$\frac{π}{4}$）=f（-x）；③f（x）在（$\frac{3π}{8}$，$\frac{π}{2}$）上是减函数．则f（x）的解析式可能是（ ）
| A． | f（x）=cos（x+$\frac{π}{8}$） | B． | f（x）=sin2x-cos2x | C． | f（x）=sinxcosx | D． | f（x）=sin2x+cos2x |
7．在△ABC中，角A，B，C所对的边分别为a，b，c，若acosA=bsinA，且B＞$\frac{π}{2}$，则sinA+sinC的最大值是（ ）
| A． | $\sqrt{2}$ | B． | $\frac{9}{8}$ | C． | 1 | D． | $\frac{7}{8}$ |
14．圆（x+2）2+（y-3）2=7的圆心与半径分别是（ ）
| A． | （2，-3），7 | B． | （-2，3），7 | C． | （2，-3），$\sqrt{7}$ | D． | （-2，3），$\sqrt{7}$ |
4．
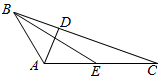如图所示，在三角形ABC中，AD⊥BC，AD=1，BC=4，点E为AC的中点，$\overrightarrow{DC}•\overrightarrow{BE}$=$\frac{15}{2}$，则AB的长度为（ ）
如图所示，在三角形ABC中，AD⊥BC，AD=1，BC=4，点E为AC的中点，$\overrightarrow{DC}•\overrightarrow{BE}$=$\frac{15}{2}$，则AB的长度为（ ）| A． | 2 | B． | $\frac{3}{2}$ | C． | $\sqrt{2}$ | D． | $\sqrt{3}$ |