题目内容
1.已知函数f(x)=alnx+$\frac{1}{x}$,a为正常数.(I)求函数f(x)的单调区间;
(Ⅱ)若对任意x1,x2∈(0,$\frac{1}{2}$],x1≠x2,都有$\frac{f({x}_{2})-f({x}_{1})}{{x}_{2}-{x}_{1}}$<-1,求a的取值范围.
分析 (1)对函数求导,由导函数的正负得到原函数的单调区间.
(2)将不等式转为为小于0的形式,构造新函数得到单调性,由单调性确定导函数的符号.从而确定a的取值范围.
解答 解:(1)∵f(x)=alnx+$\frac{1}{x}$,
∴f′(x)=$\frac{a}{x}$-$\frac{1}{{x}^{2}}$=$\frac{ax-1}{{x}^{2}}$,
∴f′(x)在区间(0,$\frac{1}{a}$)上小于0,在区间($\frac{1}{a}$,+∞)上小于0,
∴f(x)的递增区间是($\frac{1}{a}$,+∞),递减区间是(0,$\frac{1}{a}$).
(2)∵$\frac{f({x}_{2})-f({x}_{1})}{{x}_{2}-{x}_{1}}$<-1,
∴$\frac{f({x}_{2})-f({x}_{1})}{{x}_{2}-{x}_{1}}$+1<0,
即$\frac{f({x}_{2})+{x}_{2}-(f({x}_{1})+{x}_{1})}{{x}_{2}-{x}_{1}}$<0,
令h(x)=f(x)+x=alnx+$\frac{1}{x}$+x,
h′(x)=$\frac{{x}^{2}+ax-1}{{x}^{2}}$,
有题意得h′(x)≤0对任意x1,x2∈(0,$\frac{1}{2}$],x1≠x2,恒成立,
∴只需x2+ax-1≤0成立即可,
又∵当x=$\frac{1}{2}$时,y=x2+ax-1取最大值,
∴只需$\frac{1}{4}$+$\frac{1}{2}$a-1≤0恒成立,
解得a≤$\frac{3}{2}$.
点评 本题主要考察不等式的处理,移项后得到与单调性有关的式子,再由单调性确定导函数的符号,从而确定出a的取值范围.

 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案| A. | $\sqrt{2}$ | B. | $\frac{9}{8}$ | C. | 1 | D. | $\frac{7}{8}$ |
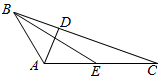 如图所示,在三角形ABC中,AD⊥BC,AD=1,BC=4,点E为AC的中点,$\overrightarrow{DC}•\overrightarrow{BE}$=$\frac{15}{2}$,则AB的长度为( )
如图所示,在三角形ABC中,AD⊥BC,AD=1,BC=4,点E为AC的中点,$\overrightarrow{DC}•\overrightarrow{BE}$=$\frac{15}{2}$,则AB的长度为( )| A. | 2 | B. | $\frac{3}{2}$ | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |