题目内容
3.已知l为双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的一条渐近线,其倾斜角为$\frac{π}{4}$,且C的右焦点为(2,0),则C的右顶点为($\sqrt{2}$,0),C的方程为$\frac{{x}^{2}}{2}$-$\frac{{y}^{2}}{2}$=1.分析 由题意可得c=2,求出渐近线方程,解方程可得a,b,即可得到右顶点和双曲线的方程.
解答 解:由题意可得c=2,即a2+b2=4,
一条渐近线的斜率为k=$\frac{b}{a}$=tan$\frac{π}{4}$=1,
解得a=b=$\sqrt{2}$,
则双曲线的右顶点为($\sqrt{2}$,0),
C的方程为$\frac{{x}^{2}}{2}$-$\frac{{y}^{2}}{2}$=1.
故答案为:($\sqrt{2}$,0),$\frac{{x}^{2}}{2}$-$\frac{{y}^{2}}{2}$=1.
点评 本题考查双曲线的顶点坐标和渐近线方程,考查运算能力,属于基础题.

练习册系列答案
相关题目
18.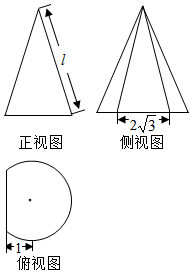 如图所示是沿圆锥的两条母线将圆锥削去一部分后所得几何体的三视图,其体积为$\frac{16π}{9}+\frac{{2\sqrt{3}}}{3}$,则圆锥的母线长为( )
如图所示是沿圆锥的两条母线将圆锥削去一部分后所得几何体的三视图,其体积为$\frac{16π}{9}+\frac{{2\sqrt{3}}}{3}$,则圆锥的母线长为( )
 如图所示是沿圆锥的两条母线将圆锥削去一部分后所得几何体的三视图,其体积为$\frac{16π}{9}+\frac{{2\sqrt{3}}}{3}$,则圆锥的母线长为( )
如图所示是沿圆锥的两条母线将圆锥削去一部分后所得几何体的三视图,其体积为$\frac{16π}{9}+\frac{{2\sqrt{3}}}{3}$,则圆锥的母线长为( )| A. | $2\sqrt{2}$ | B. | $2\sqrt{3}$ | C. | 4 | D. | $\sqrt{2}+\sqrt{3}$ |
8.已知集合A={x∈R|1≤x≤5},B={x∈R|x<2},则A∩B为( )
| A. | {x∈R|1≤x<2} | B. | {x∈R|x<1} | C. | {x∈R|2<x≤5} | D. | {x∈R|2≤x≤5} |
12.设命题甲:关于x的式x2+2ax+1>0对一切x∈R恒成立,命题乙:对数函=log(4-2a)x在(0,+∞)上递减,那么甲是乙的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
13.设全集U={x∈N|x≥2},集合A={x|x2-5x≥0},B={x|x≥3},则(∁UA)∩B=( )
| A. | {3} | B. | {3.4} | C. | {3.4,5} | D. | {3.4,5,6} |