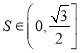题目内容
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() .
.
(1)若![]() 为等差数列,且
为等差数列,且![]()
①求该等差数列的公差![]() ;
;
②设数列![]() 满足
满足![]() ,则当
,则当![]() 为何值时,
为何值时,![]() 最大?请说明理由;
最大?请说明理由;
(2)若![]() 还同时满足:
还同时满足:
①![]() 为等比数列;
为等比数列;
②![]() ;
;
③对任意的正整数![]() 存在自然数
存在自然数![]() ,使得
,使得![]() 、
、![]() 、
、![]() 依次成等差数列,试求数列
依次成等差数列,试求数列![]() 的通项公式.
的通项公式.
【答案】(1)①![]() ;②当
;②当![]() 或
或![]() 时,
时,![]() 最大;(2)
最大;(2)![]() .
.
【解析】
(1)①利用等差数列的通项公式及前![]() 项和公式,建立方程组,即可求得该等差数列的公差
项和公式,建立方程组,即可求得该等差数列的公差![]() ;
;
②求出![]() 的通项公式,进而得到
的通项公式,进而得到![]() 的通项公式,利用
的通项公式,利用![]() ,判断
,判断![]() 的单调性,进而得解;
的单调性,进而得解;
(2)根据等比数列的性质,并结合![]() ,初步确定
,初步确定![]() 的通项,再根据等差数列的性质,即可求得
的通项,再根据等差数列的性质,即可求得![]() 的通项公式.
的通项公式.
(1)①由![]() ,
,![]() ,
,
得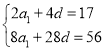 ﹐解得
﹐解得![]() ,
,![]() ,
,
该等差数列的公差![]() .
.
②由①知![]() ,所以
,所以![]() ,
,
则![]() ,
,
![]()
![]()
![]()
所以![]() ,且当
,且当![]() 时,
时,![]() 单调递增,当
单调递增,当![]() 时,
时,![]() 单调递减,
单调递减,
故当![]() 或
或![]() 时,
时,![]() 最大.
最大.
(2)因为![]() 是等比数列,则
是等比数列,则![]() ,
,
又![]() ,
,
所以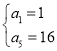 或
或 ,
,
由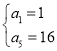 ,得
,得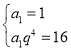 ,解得
,解得![]() ,
,
由 ,得
,得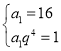 ,解得
,解得![]() ,
,
从而![]() 或
或![]() 或
或![]() 或
或![]() ,
,
又因为![]() 、
、![]() 、
、![]() 依次成等差数列,得
依次成等差数列,得![]() ,而公比
,而公比![]() ,
,
所以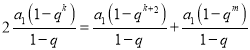 ,即
,即![]() ,
,
从而![]() (*)
(*)
当![]() 时,(*)式不成立;
时,(*)式不成立;
当![]() 时,解得
时,解得![]() ;
;
当![]() 时,(*)式不成立;
时,(*)式不成立;
当![]() 时,(*)式不成立.
时,(*)式不成立.
综上所述,满足条件的![]() .
.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目