题目内容
设O为△ABC的外心,且 ,则△ABC中的内角C值为
,则△ABC中的内角C值为
- A.

- B.

- C.

- D.

B
分析:由 ,移项得
,移项得 ,再平方得:
,再平方得: ,得到
,得到 =0,从而
=0,从而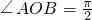 ,最后根据圆心角等于同弧所对的圆周的两倍得△ABC中的内角C值.
,最后根据圆心角等于同弧所对的圆周的两倍得△ABC中的内角C值.
解答:设外接圆的半径为R,
∵ ,
,
∴ ,
,
∴ ,
,
∴25R2+24 =25R2,
=25R2,
∴ =0,
=0,
∴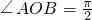 ,
,
根据圆心角等于同弧所对的圆周的两倍得:
△ABC中的内角C值为= .
.
故选B.
点评:本小题主要考查三角形外心的应用、向量在几何中的应用等基础知识,考查运算求解能力与转化思想.属于基础题.
分析:由
 ,移项得
,移项得 ,再平方得:
,再平方得: ,得到
,得到 =0,从而
=0,从而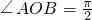 ,最后根据圆心角等于同弧所对的圆周的两倍得△ABC中的内角C值.
,最后根据圆心角等于同弧所对的圆周的两倍得△ABC中的内角C值.解答:设外接圆的半径为R,
∵
 ,
,∴
 ,
,∴
 ,
,∴25R2+24
 =25R2,
=25R2,∴
 =0,
=0,∴
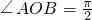 ,
,根据圆心角等于同弧所对的圆周的两倍得:
△ABC中的内角C值为=
 .
.故选B.
点评:本小题主要考查三角形外心的应用、向量在几何中的应用等基础知识,考查运算求解能力与转化思想.属于基础题.

练习册系列答案
相关题目
设O为△ABC的外心,且3
+4
+5
=
,则△ABC中的内角C值为( )
| OA |
| OB |
| OC |
| 0 |
A、
| ||
B、
| ||
C、
| ||
D、
|