题目内容
若直角坐标平面内A、B两点满足:①点A、B都在函数f(x)的图象上;②点A、B关于原点对称,则这两点A、B构成函数f(x)的一个“姊妹点对”,已知函数f(x)=
,则f(x)的“姊妹点对”有 个.
|
考点:分段函数的应用
专题:新定义,函数的性质及应用
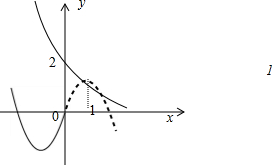
分析:根据题意可知,只需作出函数y=x2+2x(x<0)的图象关于原点对称的图象,看它与函数y=
(x≥0)交点个数即可.观察图象可得.
| 2 |
| ex |
解答:
 解:根据题意可知,“姊妹点对”满足两点:都在函数图象上,且关于坐标原点对称.
解:根据题意可知,“姊妹点对”满足两点:都在函数图象上,且关于坐标原点对称.
可作出函数y=x2+2x(x<0)的图象关于原点对称的图象,看它与函数y=
(x≥0)交点个数即可.如图所示:当x=1时,0<
<1.
观察图象可得:它们有2个交点.
故答案为:2.
 解:根据题意可知,“姊妹点对”满足两点:都在函数图象上,且关于坐标原点对称.
解:根据题意可知,“姊妹点对”满足两点:都在函数图象上,且关于坐标原点对称.可作出函数y=x2+2x(x<0)的图象关于原点对称的图象,看它与函数y=
| 2 |
| ex |
| 2 |
| e |
观察图象可得:它们有2个交点.
故答案为:2.
点评:本题主要考查了奇偶函数图象的对称性,以及数形结合的思想,解答的关键在于对“姊妹点对”的正确理解,合理地利用图象法解决.

练习册系列答案
相关题目
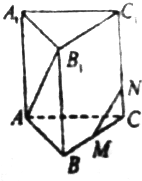 正三棱柱ABC-A1B1C1的侧棱长为2,底面边长为1,点M是BC的中点.
正三棱柱ABC-A1B1C1的侧棱长为2,底面边长为1,点M是BC的中点.