��Ŀ����
17��.�мס��ҡ���������֧��ӽ��е�ѭ�����������ݸ��ӻ��־������Σ��涨ÿ�������������ʤ��������ʤ����2�֣�������1�֣���֪��Ӽ�������Ҷ���ȡʤ�ĸ���Ϊ$\frac{2}{5}$������ӱ���������ȡʤ�ĸ��ʾ�Ϊ$\frac{1}{2}$���Ҹ�����ʤ������˴�û��Ӱ�죮��1��������ʤһ���ĸ��ʣ�
��2������Ӽ�������֦εĸ��ʷֲ�����ѧ������
���� ��1��������ʤһ���Ķ����¼��Ǽ���������ȫ�����ɴ����ö����¼����ʼ��㹫ʽ�����������ʤһ���ĸ��ʣ�
��2��������֪��Ӽ�������֦εĿ���ȡֵΪ3��4��5��6���ֱ������Ӧ�ĸ��ʣ��ɴ�������εķֲ��к���ѧ������
��� �⣺��1������Ӽ�������Ҷ���ȡʤ�ĸ���Ϊ$\frac{2}{5}$��
����ӱ���������ȡʤ�ĸ��ʾ�Ϊ$\frac{1}{2}$��
�Ҹ�����ʤ������˴�û��Ӱ�죮
������ʤһ���Ķ����¼��Ǽ���������ȫ����
�������ʤһ���ĸ���p=1-��1-$\frac{2}{5}$����1-$\frac{1}{2}$����1-$\frac{1}{2}$��=$\frac{17}{20}$��
��2��������֪��Ӽ�������֦εĿ���ȡֵΪ3��4��5��6��
P����=3��=��1-$\frac{2}{5}$����1-$\frac{1}{2}$����1-$\frac{1}{2}$��=$\frac{3}{20}$��
P����=4��=$\frac{2}{5}$��1-$\frac{1}{2}$����1-$\frac{1}{2}$��+��1-$\frac{2}{5}$����$\frac{1}{2}$����1-$\frac{1}{2}$��+��1-$\frac{2}{5}$������1-$\frac{1}{2}$����$\frac{1}{2}$=$\frac{2}{5}$��
P����=5��=$\frac{2}{5}$��$\frac{1}{2}$����1-$\frac{1}{2}$��+��1-$\frac{2}{5}$����$\frac{1}{2}$��$\frac{1}{2}$+$\frac{2}{5}$����1-$\frac{1}{2}$����$\frac{1}{2}$=$\frac{7}{20}$��
P����=6��=$\frac{2}{5}$��$\frac{1}{2}$��$\frac{1}{2}$$\frac{1}{10}$��
��εķֲ���Ϊ��
| �� | 3 | 4 | 5 | 6 |
| P | $\frac{3}{20}$ | $\frac{2}{5}$ | $\frac{7}{20}$ | $\frac{1}{10}$ |
���� ���⿼����ɢ����������ķֲ��к���ѧ��������������ʵ���Ӧ�ã����鿼��������֤�����������������������ת������˼�룬���е��⣮

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�| A�� | $\frac{{\sqrt{2}}}{2}$ | B�� | $\frac{1}{2}$ | C�� | $\frac{{\sqrt{3}}}{3}$ | D�� | ����ȷ�� |
| A�� | b1b2��bn=b1b2��b17-n����n��17��n��N*�� | |
| B�� | b1b2��bn=b1b2��b18-n��n��18��n��N*�� | |
| C�� | b1+b2+��+bn=b1+b2+��+b17-n��n��17��n��N*�� | |
| D�� | b1+b2+��+bn=b1+b2-1+��+b18-n��n��18��n��N*�� |
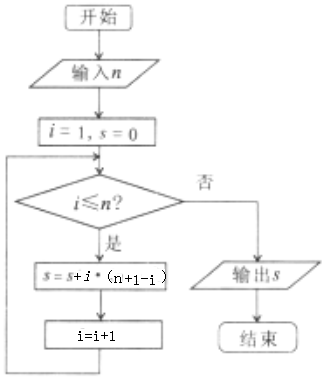
| A�� | 10 | B�� | 16 | C�� | 20 | D�� | 35 |
| A�� | $\frac{1}{10}$ | B�� | 0 | C�� | -10 | D�� | -15 |
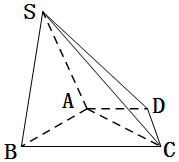 ��ͼ����ͼ��������S-ABCD�У���������ABCD�У�BC��AD��ƽ��SAB��ƽ��ABCD����SAB�ǵȱ������Σ���֪$AC=2AB=4��BC=2AD=2DC=2\sqrt{5}$��
��ͼ����ͼ��������S-ABCD�У���������ABCD�У�BC��AD��ƽ��SAB��ƽ��ABCD����SAB�ǵȱ������Σ���֪$AC=2AB=4��BC=2AD=2DC=2\sqrt{5}$��