题目内容

已知f(x)=2sin(2x-
π
6
)-m在x∈[0，
π
2
]上有两个不同零点，则m的取值范围为（　　）
A、（1，2）
B、[1，2]
C、[1，2）
D、（1，2]
分析：f(x)=2sin(2x-
π
6
)-m在x∈[0，
π
2
]上有两个不同零点，可转化为y=2sin(2x-
π
6
)与y=m在x∈[0，
π
2
]上有两个不同交点，作出图象，由图得出m的取值范围
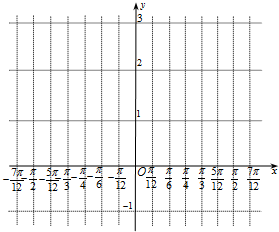
解答：精英家教网解：f(x)=2sin(2x-
π
6
)-m在x∈[0，
π
2
]上有两个不同零点可转化为y=2sin(2x-
π
6
)与y=m在x∈[0，
π
2
]上有两个不同交点，作出如图的图象，
由于右端点的坐标是（
π
2
，1）
由图知，m∈[1，2）
故选C
点评：本题考查正弦函数的图象，解答本题关键是将函数有两个零点的问题转化为两个函数有两个交点的问题，作出两函数的图象，判断出参数的取值范围，本题以形助数，是解此类题常用的方法，熟练作出相应函数的图象对解答本题很重要．
练习册系列答案
相关题目
已知f(x)=2sin(x-
π
4
)•cos(x-
π
4
)+sin2x，则函数f（x）得最小正周期是
 
．
已知f(x)=
2
sin(2x-
π
4
)，x ∈[
π
4
，
5π
4
]
（Ⅰ）用五点作图法作出f（x）的图象，并指出函数的单调区间和值域；
（Ⅱ）若f（x）=a有两个不同的实数根，请你求出这两根之和．
已知f(x)=2sin(2x-
π
6
)-m在x∈[0，
π
2
]上有两个不同的零点x1，x2，则m取值范围是
[1，2）
[1，2）
，x1+x2=
2π
3
2π
3
．
已知f(x)=2sin(
π
6
-2x)+a．
（1）求f（x）的单调递增区间；
（2）若f（x）的定义域为(-
π
4
，0)时，最大值为3，求a的值．
精英家教网已知f(x)=2sin(2x-
π
3
)+1．
（1）求f（x）的单调增区间；
（2）求f（x）图象的对称轴的方程和对称中心的坐标；（3）在给出的直角坐标系中，请画出f（x）在区间[-
π
2
，
π
2
]上的图象．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网